丹德林球
在几何学中,丹德林球是指一个或两个球体,它们与圆锥相切,同时也与另一个与此圆锥相交的平面相切。圆锥与平面的截㡾则形成圆锥曲线,而任一球体与平面相接的点则是圆锥曲线的焦点。因此丹德林球有时也称为焦球。
丹德林球是在 1822 年发现的。[1] 它是为纪念法国数学家当德兰·皮埃尔·丹德林(Germinal Pierre Dandelin)而名, 但朗伯·阿道夫·雅克·凯特勒 也有部分贡献。[2]
丹德林球的用途,通常是用来为已阿波罗尼奥斯所知的两个定理提供优雅的现代证明。第一个定理是,所有与两个固定点(焦点)的距离之和是常数的点,其轨迹是闭合圆锥曲线(即椭圆)。第二个定理是,对于任圆锥曲线,到定点(焦点)的距离与到定线(准线)的距离成正比,比例常数称为偏心率。 [3]
圆锥曲线的每个焦点都会有一个丹德林球。椭圆有两个丹德林球,它们会相切于相同的锥体,而双曲线则有两个丹德林球,却是接触相反的锥体。抛物线则只有一个丹德林球。
截面曲线到焦点的距离之和为定值的证明
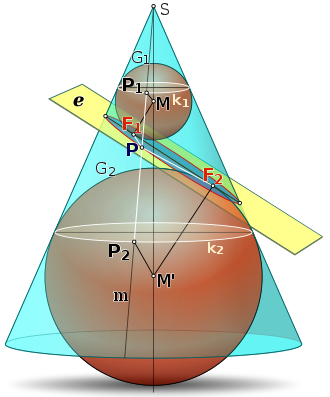
编辑解释如下,设 S 为此圆锥的顶点,平面 e 与此圆锥交于曲线 C(蓝色区域)。以下则证明 C 是椭圆。
放置两个棕色的丹德林球G1 和 G2,皆与平面和圆锥相交,上面的为G1,下面的为G2。而两个球体与锥体相切的点形成圆形(白色的部分),分别记为 与 。
将 G1 与此平面的切点记为 F1 ;类似地,用于G2 与F2。P 为曲线 C 上一点。
需要证明:当 P 沿着截面曲线 C 移动时, 仍是定值(椭圆的定义之一)。
- 将 P 与圆锥顶点 S 作一直线,与 G1 和 G2 分别交于 P1 和 P2 。
- 将 P 移动时,P1 和 P2 则沿着两个圆移动,且其距离 是定值。
- P 和 F1 的距离会等同于 P 到 P1 的距离,因为线段 PF1 和 PP1 都相切于G1。
- 基于对称性,P 到 F2 的距离,等于 P 到 P2 的距离,因为线段 PF2 和 PP2 都相切于G2
- 于是,我们计算出其距离和 是定值。
这是用以证明阿波罗尼奥斯定理的另一个证明。
如果我们定义椭圆为与两交点的距离和为定义的 P 的集合,则上述论述证明了此曲线确实是椭图。此面,平面与圆锥截痕会以 F1 和 F2 的中垂线对称这论述,看起来像是违反直觉,但此方法则让其显而易见。的则是因为焦点可互换。
焦点-准线性质的证明
编辑丹德林球同样也可用来发现圆锥截面的准线。每个丹德林球与㘣锥相切的点会形成圆形,而由这些圆形可定义出它的所在的平面且平行。 而它们与原平面的截痕则会是平行线,此即为准线。然而,抛物线则会有一个丹德林球,因此只有一个准线。
使用丹德林球,可以证明此截痕:“与焦点的距离和准线的距离成比例”。[4] 古希腊数学家,如阿波罗尼奥斯 ,认知到此性质,而丹德林球则给出了证明。[3]
但丹德林或Quetelet 都没使用丹德林球来证明此属性。第一个如此做的人可能是 1829 年的 Pierce Morton[5],又或者可能是 Hugh Hamilton (bishop) 在 1758 年时记下的“一个与圆锥相切于球,可用来定义了一个新平面,与原平面的截痕即为准线”。[1][6][7][8]而焦点-准线性质也可提供一个简单的作法,可以用来证明开普勒定律。[9]
外部链接
编辑- ^ 1.0 1.1 Dandelin, G. Mémoire sur quelques propriétés remarquables de la focale parabolique [Memoir on some remarkable properties of the parabolic focale [i.e., oblique strophoid]. Nouveaux mémoires de l'Académie royale des sciences et belles-lettres de Bruxelles. 1822, 2: 171–200 [2021-10-28]. (原始内容存档于2021-11-13) (法语).
- ^ Godeaux, L. Le mathématicien Adolphe Quetelet (1796-1874). Ciel et Terre. 1928, 44: 60–64 [2021-10-28]. (原始内容存档于2021-10-28) (法语).
- ^ 3.0 3.1 Heath, Thomas. A History of Greek Mathematics, page 119 (focus-directrix property) (页面存档备份,存于互联网档案馆), page 542 (sum of distances to foci property) (页面存档备份,存于互联网档案馆) (Clarendon Press, 1921).
- ^ Brannan, A. et al. Geometry, page 19 (页面存档备份,存于互联网档案馆) (Cambridge University Press, 1999).
- ^ Numericana's Biographies: Morton, Pierce. [2021-10-29]. (原始内容存档于2022-01-21).
- ^ Morton, Pierce. Geometry, Plane, Solid, and Spherical, in Six Books, page 228 (页面存档备份,存于互联网档案馆) (Baldwin and Cradock, 1830).
- ^ Morton, Pierce. On the focus of a conic section. Transactions of the Cambridge Philosophical Society. 1830, 3: 185–190 [2021-10-29]. (原始内容存档于2021-11-03).
- ^ Hamilton, Hugh. De Sectionibus Conicis. Tractatus Geometricus. In quo, ex Natura ipsius Coni, Sectionum Affectiones facillime deducuntur. Methodo nova. [On conic sections. A geometric treatise. In which, from the nature of the cone itself, relations of sections are most easily deduced. By a new method.]. London, England: William Johnston. 1758: 122–125 (拉丁语). Liber (book) II, Propositio (proposition) XXXVII (37).
- ^ Hyman, Andrew. "A Simple Cartesian Treatment of Planetary Motion", European Journal of Physics, Vol. 14, page 145 (页面存档备份,存于互联网档案馆) (1993).