欧姆定律
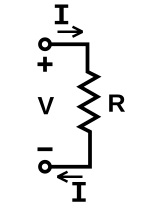
在电路学里,欧姆定律(英语:Ohm's law)表明:定温下,电导体两端的电压 与通过电导体的电流 成正比[1]。数学表达式为:
因此,对于任意电导体(电路、电路元件、甚至电阻器),电阻 可定义为此正比关系的比例常数[1]:
且可得到下列方程式:
不论电流、电压为何,电阻定义均为电压除以电流。此外,任何电导体都有电阻,即使超导体在一般温度下也具有微小的电阻。
然而并不是每一种元件都遵守欧姆定律,此定律是经过多次实验而推断的法则,只有在理想状况下,才会成立。凡是遵守欧姆定律的元件或电路都称为“欧姆元件”或“欧姆电路”或“欧姆式导体”,其电阻与电流、电压的变动无关;不遵守欧姆定律的元件或电路称为“非欧姆元件”或“非欧姆电路”或“非欧姆式导体”,其电阻可能会与电流、电压的变动有关。
欧姆定律是因德国物理学家格奥尔格·欧姆命名。于1827年,在他发表的一本通论《直流电路的数学研究》(The galvanic Circuit investigated mathematically)里[2],他详细的论述简单电路两端的电压与流动于电路的电流之间的关系。他所论述的关系比较复杂,稍后会有更详细说明。上述方程式乃是欧姆定律的现代版本。
对于电阻物质或导电物质,欧姆定律可以推广为:
其中,是电场,是物质的电流密度,是物质的电阻率,是物质的电导率。
遵守欧姆定律的物质,称为“欧姆物质”,其电阻率和电导率与电流密度、电场无关[1]。
历史
编辑早于1753年,意大利物理学家乔凡尼·贝卡立亚就在研究物质的导电性质。他在电路里加装了盛满了水的玻璃管。当开启电路后,发现玻璃管的截面面积越大,电流的放电强度越大[3]。
英国物理学家亨利·卡文迪什也曾做过很多实验,研究电动势、电流、电阻之间的关系。他使用莱顿瓶为电流源,将电流通过在各种尺寸的玻璃试管里盛装的盐溶液,靠著调整盐溶液的高度,他可以控制放电强度。卡文迪什把自己身体当作一台生理检流计,从亲身体验被电击后的感觉,来估计电流的放电强度。他又选择出一个装满盐溶液的玻璃试管为标准,然后比较标准放电与试样放电,按照放电强度的大小来估计它们的电阻。这样,他可以定量地描述每一种试样。于1781年1月,他记录在笔记里,电流与电动势成正比。但是,他并没有将这些珍贵的实验结果告诉任何科学家。一直到马克士威于1879年替他编辑注释为著作《卡文迪什的电学研究》(The electrical researches of the Honourable Henry Cavendish)后,才见诸世面[4][5]。注意到卡文迪什使用的仪器相当原始粗陋,靠身体感觉很难做出精准的测量,莱顿瓶并不是稳定电流源。所以,学术界认为这耽搁了近百年的实验结果并不足以证实欧姆定律。
从1825年到1826年之间,欧姆做了很多关于电阻的实验。于1827年,他将得到的结果一同发表在著作《直流电路的数学研究》(The galvanic Circuit investigated mathematically)里[6]。他从傅立叶对于热传导的研究得到了相当多的灵感,借用了很多傅立叶的点子来论述自己的结果。
欧姆是一位优秀的实验者,很会设计与制造实验设备,又具有精湛的数学修养与严谨的敬业态度。刚开始,他使用伏打电堆为电源,用安装于扭秤(torsion balance)的磁针来测量电流的磁场力。载流导线的电流所产生的磁场与电流成正比,只要测量在载流导线附近的磁针所感受到的磁场力,就可以知道电流。他将电流通过不同长度的检验电线;由于长度不同,电阻也不同。欧姆仔细分析实验结果,得到经验方程式[7] [8]
其中, 是检验电线造成的电流差值, 是跟实验参数有关的系数, 是检验电线的长度, 是跟固定长度的载流导线有关的常数。
欧姆很快地就觉得这方程式不太对劲。大约三年前,汤玛斯·泽贝克发明使用热电偶为电源。这种电源比伏打电源稳定。采纳《物理与化学年鉴》的总编辑约翰·波根多夫(Johann poggendorff)的建议,欧姆改用热电偶为电源[9][10],将实验重做一遍,得到经验方程式:
其中, 是扭秤读值, 是跟电动势有关的常数, 是跟内部电阻有关的常数, 是检验电线的长度。
仔细诠释这些变量,将 、 、 、 分别诠释为电流 、电压 、内部电阻 、检验电阻 ,那么,假定总电阻 为 则经验方程式变为欧姆定律的现代方程式版本:
欧姆定律可能是早期电学史最重要的定量理论。但是,当欧姆最初发表他的结果时,很多学术界同仁都激烈地批评反对他的理论。德国教育部长指责:“鼓吹这种异端邪说的教授不配教导科学[11]。”物理教授格奥尔格·魄尔(Georg Pohl)这样批评欧姆的著作:“以崇高眼光仰看这世界的人士,必须远离这本无可救药、妄生穿凿的谬书,其唯一目的乃是彻底诋毁大自然的尊严[7]。”。那时候,德国正盛行的黑格尔哲学认为,因为大自然井井有序,而且只要经过合理推论就可获得科学真理,所以,并不需要靠做实验来了解大自然。欧姆的实验方法可能引起了黑格尔门徒的强烈反感。
1839年,法国物理学家,克劳德·普雷特(Claude Pouillet)确定欧姆的实验结果。同时,欧姆成为柏林科学院的院士。在英国,查尔斯·惠斯通又重新核对了欧姆的实验结果。1841年,欧姆被选为皇家学会的外籍会员。1852年,欧姆荣膺为慕尼黑大学的物理学系主任。
于1920年,物理学家发现,通过理想电阻器的电流会出现统计涨落,虽然当电压和电阻为常数时,统计涨落会跟温度有关。这种涨落称为詹森-奈奎斯特噪音(Johnson–Nyquist noise),是因为电荷的离散秉性而产生的现像。这热效应意味著,假若取样的时间间隔足够短暂,电流或电压的测值,其比例跟时间平均比例或系综平均(ensemble average)比例相比较,会出现涨落;也就是说,每一个电阻 的取样值,跟 的时间平均或系综平均相比较,会出现涨落。对于普通电阻物质案例,经过平均程序后,欧姆定律仍旧正确无误。
欧姆对于电阻的研究在马克士威方程组出现之前很久,那时科学家对于交流电路的频率相关效应也不了解。但是,在适当范围内,现代电磁理论与现代电路理论并没有发现任何与欧姆定律相悖之处。
水力学类比
编辑欧姆定律可以用水力学类比(hydraulic analogy)来描述。测量单位为帕斯卡的水压,可以类比为电压。在一根水管里,由于任意两点之间的水压差会造成水流,水的流速(单位是公升每秒),可以类比为电流(单位是库仑每秒)。“流量限制器”是安装于水管与水管之间控制流量的阀门,可以类比为电阻器。通过流量限制器的水流流量,跟流量限制器两端的水压成正比,类似地,通过电阻器的电荷流量(电流),跟电阻器两端的电压成正比。这正是欧姆定律的论述。
流体流动网路的流量和流压可以用水力学类比方法来计算[12][13]。这方法可以应用于稳定流和暂态流(transient flow)。对于线性层流,泊肃叶定律(Poiseuille's law)描述水管的水阻,但是对于湍流,流压-流量关系变为非线性。
热力学类比
编辑设定电导体的电导率与两端的电压,欧姆定律可以预测出通过这电导体的电流密度。类似地,设定热导体的热导率与两端的温差,约瑟夫·傅立叶的热传导定律可以预测通过这热导体的热流[14]。同样的方程式形式可以描述这两种现象。对于每一种案例,方程式的变量有不同的意义。具体而言,欧姆定律的方程式为:
而热传导定律的方程式为:
其中, 是热通量(heat flux), 是导热体的热导率, 是温度。
思考参数为温度、热导率与热通量的热传导问体,和参数为电压、电导率与电流密度的电传导问体。这两个问题相互等价。假若能够解析一个热传导问体,则也能够解析电传导问题;反之亦然。
电路分析
编辑在电路学里,电阻器(欧姆电阻器)是一种电路元件,其电阻与电压、电流无关。电阻器可以按照欧姆定律阻抗电荷的通过。每一个电阻器都有其设计制成的电阻 。更严格地说,电阻器是在某操作域内遵守欧姆定律的电路元件;欧姆定律和唯一电阻值足够描述这元件在相关操作域的行为。
串联电阻电路
编辑串联电阻的总电阻等于各个电阻之和,以方程式表示,
其中, 是第 个电阻, 是总电阻。
假设在电路两端的电压为 ,则通过的电流为 。假设每一个电阻器都遵守欧姆定律,则这电路是电阻为 的欧姆电路。
并联电阻电路
编辑相互并联的电阻,其总电阻的倒数等于其每个电阻的倒数和,以方程式表示:
假设在电路两端的电压为 ,则通过的电流为 。假设每一个电阻器都遵守欧姆定律,则这电路是电阻为 的欧姆电路。
周期性激发
编辑电容器、电感器、传输线等等,都是电路的电抗元件。假设施加周期性电压或周期性电流于含有电抗元件的电路,则电压与电流之间的关系式变成微分方程式。因为欧姆定律的方程式只涉及实值的电阻,不涉及可能含有电容或电感的复值阻抗,所以,前面阐述的欧姆定律不能直接应用于这状况。
最基本的周期性激发,像正弦激发或馀弦激发,都可以用指数函数来表达:
假设周期性激发为单频率正弦激发,其角频率为 。电阻为 的电阻器,其阻抗 为:
电感为 的电感器,其阻抗为:
电容为 的电容器,其阻抗为:
电压 与电流 的关系式为:
注意到将阻抗 替代电阻 ,就可以得到这欧姆定律方程式的推广。只有 的实值部分会造成热能的耗散。
对于这系统,电流和电压的复值波形式分别为:
电流和电压的实值部分 、 分别描述这电路的真实正弦电流和正弦电压。由于 、 都是不同的复值纯量,电流和电压的相位可能会不一样。
周期性激发可以傅立叶分解为不同角频率的正弦函数激发。对于每一个角频率的正弦函数激发,可以使用上述方法来计算响应。然后,将所有响应总和起来,就可以得到解答。
线性近似
编辑欧姆定律是电路分析(circuit analysis)使用的几个基本方程式之一。它可以应用于金属导电体或特别为这行为所制备的电阻器。在电机工程学里,这些东西无所不在。遵守欧姆定律的物质或元件称为“欧姆物质”或“欧姆元件”。理论上,不论施加的电压或电流、不论是直流或交流、不论是正极或负极,它们的电阻都不变[15]。
但是,有些电路元件不遵守欧姆定律,它们的电压与电流之间的关系(V-I线)乃非线性关系。PN接面二极体是一个显明范例。如右图所示,随著二极体两端电压的递增,电流并没有线性递增。给定外电压,可以用V-I线来估计电流,而不能用欧姆定律来计算电流,因为电阻会因为电压的不同而改变。另外,只有当外电压为正值时,电流才会显著地递增;当施加的电压为负值时,电流等于零。对于这类元件,V-I线的斜率 ,称为“小信号电阻”(small-signal resistance)、“增量电阻”(incremental resistance)或“动态电阻”(dynamic resistance),定义为
温度效应
编辑詹姆斯·马克士威诠释欧姆定律为,处于某状态的导电体,其电动势与产生的电流成正比。因此,电动势与电流的比例,即电阻,不会随著电流而改变。在这里,电动势就是导电体两端的电压。参考这句引述的上下文,修饰语“处于某状态”,诠释为处于常温状态,这是因为物质的电阻率通常跟温度有关。根据焦耳定律,导电体的焦耳加热(Joule heating)与电流有关,当传导电流于导电体时,导电体的温度会改变。电阻对于温度的相关性,使得在典型实验里,电阻跟电流有关,从而很不容易直接核对这形式的欧姆定律。于1876年,马克士威与同事,共同设计出几种测试欧姆定律的实验方法,能够特别凸显出导电体对于加热效应的响应[17]。
其它版本的欧姆定律
编辑在电机工程学和电子工程学里,欧姆定律妙用无穷,因为它能够在宏观层次表达电压与电流之间的关系,即电路元件两端的电压与通过的电流之间的关系。在物理学里,对于物质的微观层次电性质研究,会使用到的欧姆定律,以向量方程式表达为:
在导体内任意两点g、h,定义电压为将单位电荷从点g移动到点h,电场力所需做的机械功:[18]
其中, 是电压, 是机械功, 是电荷量, 是微小线元素。
假设,沿著积分路径,电流密度 为均匀电流密度,并且平行于微小线元素:
其中, 是积分路径的单位向量。
那么,可以得到电压:
其中, 是积分路径的径长。
假设导体具有均匀的电阻率,则通过导体的电流密度也是均匀的:
其中, 是导体的截面面积。
电压 简写为 。电压与电流成正比:
总结,电阻与电阻率的关系为:
假设 ,则 ;将单位电荷从点g移动到点h,电场力需要作的机械功 。所以,点g的电势比点h的电势高,从点g到点h的电势差为 。从点g到点h,电压降是 ;从点h到点g,电压升是 。
给予一个具有完美晶格的晶体,移动于这晶体的电子,其运动等价于移动于自由空间的具有有效质量(effective mass)的电子的运动。所以,假设热运动足够微小,周期性结构没有偏差,则这晶体的电阻等于零。但是,真实晶体并不完美,时常会出现晶体缺陷(crystallographic defect),有些晶格点的原子可能不存在,可能会被杂质侵占。这样,晶格的周期性会被扰动,因而电子会发生散射。另外,假设温度大于绝对温度,则处于晶格点的原子会发生热震动,会有热震动的粒子,即声子,移动于晶体。温度越高,声子越多。声子会与电子发生碰撞,这过程称为晶格散射(lattice scattering)。主要由于上述两种散射,自由电子的流动会被阻碍,晶体因此具有有限电阻[19]。
凝聚态物理学研究物质的性质,特别是其电子结构。在凝聚态物理学里,欧姆定律更复杂、更广义的方程式非常重要,属于本构方程式(constitutive equation)与运输系数理论(theory of transport coefficients)的范围。
经典微观表述
编辑当施加外电场于导电体时,电流密度的响应,基本上是属于量子力学性质。详尽细节,请参阅经典与量子电导率(classical and quantum conductivity)。保罗·德鲁德于1900年研究出的德鲁德模型,可以用经典物理解释欧姆定律,描述自由电子移动于金属导电体的物理行为[20] [21]。
在德鲁德模型里,自由电子会不停地移动碰撞于固定不动、组成整个金属导电体晶格的正价离子之间。金属里的每一个自由电子,感受到电场力的作用,会呈加速运动。但是每当自由电子与晶格发生碰撞,其动能会遭受损失,以热能的形式将能量释放给离子,所以,电子的平均移动速度是漂移速度,其漂移速度的方向与电场方向相反。
电子感受到的平均电场力 为:
其中, 是平均电场, 是单位电荷量。
德鲁德计算出漂移速度 为:
其中, 是平均自由时间(mean free time),是碰撞之间的平均时间间隔, 是电子的质量。
在金属里,电荷载子为电子,所以电流密度与漂移速度的关系为:
其中, 是电子密度。
假设电场是均匀电场, ,设定电阻率为:
则电场与电流密度的关系为:
注意到漂移速率 超小于热速率 ,
因此,平均自由时间与热速率有关,与漂移速率无关,所以平均自由时间也与电流密度、电场无关。质量、电子密度、单位电荷,都与电流密度、电场无关。总结,电阻率与电流密度、电场无关。
磁效应
编辑前面得到的答案只成立于导电体的参考系。在经典电磁学里,假设处于磁场 的导电体,以相对速度 移动于磁场的参考系 ,则电子感受到的平均劳仑兹力 为:
漂移速度 为:
电场与电流密度的关系为:
所以,欧姆定律的形式推广为:
常见错误
编辑不少人会认为欧姆定律是在说明
实际上,上式只是电阻的定义,而欧姆定律所主张的是任何物件都会满足
是一个错误的主张。(仅对部分欧姆式导体正确)[22]
参阅
编辑参考文献
编辑- ^ 1.0 1.1 1.2 Halliday, David; Robert Resnick, Jearl Walker, Fundamental of Physics 7th, USA: John Wiley and Sons, Inc.: pp. 691–692, 2005, ISBN 0-471-23231-9
- ^ 欧姆, 格奥尔格, The Galvanic Circuit Investigated Mathematically, New York: D. Van Nostrand Company, 1891
- ^ Whittaker, E. T., A history of the theories of aether and electricity. Vol 1, Nelson, London: pp. 53, 1951
- ^ Electricity, Encyclopedia Britannica, 1911, (原始内容存档于2008-09-15)
- ^ Sanford P. Bordeau (1982) Volts to Hertz...the Rise of Electricity. Burgess Publishing Company, Minneapolis, MN. pp.86–107, ISBN 978-0-8087-4908-0
- ^ G. S. Ohm, The galvanic Circuit investigated mathematically, D. Van Nostrand Company, 1891
- ^ 7.0 7.1 Hammond, P., Georg Simon Ohm and his law (PDF), Jounal of the Institution of Electrical Engineers, June 1958, 4 (42): pp. 294–296[永久失效链接]
- ^ Gupta, Madhu Sudan, Georg Simon Ohm and Ohm's Law, IEEE Transactions on Education, Aug 1980, 23 (3): pp. 156–162
- ^ Shedd, John C.; Hershey, Mayo D., The History of Ohm's Law, Popular Science Monthly (Bonnier Corporation), 1913: pp. 599ff
- ^ Keithley, Joseph F., The story of electrical and magnetic measurements: from 500 B.C. to the 1940s, John Wiley and Sons: pp.93ff, 102, 1999, ISBN 9780780311930
- ^ Pickover, Clifford, Archimedes to Hawking: laws of science and the great minds behind them, U.S.A.: Oxford University Press: pp. 8, 2008, ISBN 9780195336115
- ^ A. Akers, M. Gassman, & R. Smith. Hydraulic Power System Analysis. New York: Taylor & Francis. 2006: Chapter 13. ISBN 0-8247-9956-9.
- ^ A. Esposito, "A Simplified Method for Analyzing Circuits by Analogy", Machine Design, October 1969, pp. 173–177.
- ^ 傅立叶, 约瑟夫, The Analytical Theory of Heat, Cambridge University Press, 2009 [1878], ISBN 978-1-108-00178-6
- ^ Hughes, E, Electrical Technology, pp10, Longmans, 1969.
- ^ Horowitz, Paul; Winfield Hill. The Art of Electronics 2nd. Cambridge University Press. 1989: 13. ISBN 0-521-37095-7.
- ^ Normal Lockyer (编). Reports. Nature (Macmillan Journals Ltd). September 21, 1876, 14: 452.
- ^ Alexander, Charles; Sadiku, Matthew, fundamentals of Electric Circuits 3, revised, McGraw-Hill: pp. 9–10, 2006, ISBN 9780073301150
- ^ Seymour J, Physical Electronics, pp 48–49, Pitman, 1972
- ^ Drude, Paul. Zur Elektronentheorie der metalle. Annalen der Physik. 1900, 306 (3): 566. doi:10.1002/andp.19003060312.[永久失效链接]
- ^ Drude, Paul. Zur Elektronentheorie der Metalle; II. Teil. Galvanomagnetische und thermomagnetische Effecte. Annalen der Physik. 1900, 308 (11): 369. doi:10.1002/andp.19003081102.[永久失效链接]
- ^ Principles of Physics 11th Edition, by David Halliday, Robert Resnic, Jearl Walker, page 26-13












