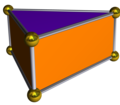
三角柱
在幾何學中,三角柱是一種柱體,底面為三角形。正三角柱是半正多面體、均勻多面體的一種。
 | |||||
| 類別 | 柱體 柱狀均勻多面體 | ||||
|---|---|---|---|---|---|
| 對偶多面體 | 雙三角錐 | ||||
| 識別 | |||||
| 名稱 | 正三角柱 | ||||
| 參考索引 | U76(a) | ||||
| 鮑爾斯縮寫 | trip | ||||
| 數學表示法 | |||||
| 考克斯特符號 | |||||
| 施萊夫利符號 | t{2,3} {3}×{} | ||||
| 威佐夫符號 | 2 3 | 2 | ||||
| 康威表示法 | P3 | ||||
| 性質 | |||||
| 面 | 5 | ||||
| 邊 | 9 | ||||
| 頂點 | 6 | ||||
| 歐拉特徵數 | F=5, E=9, V=6 (χ=2) | ||||
| 組成與佈局 | |||||
| 面的種類 | 2個三角形 3個正方形 | ||||
| 面的佈局 | 3{4}+2{3} | ||||
| 頂點圖 | 4.4.3 | ||||
| 對稱性 | |||||
| 對稱群 | D3h, [3,2], (*322), order 12 | ||||
| 旋轉對稱群 | D3, [3,2]+, (322), order 6 | ||||
| 特性 | |||||
| 凸 | |||||
| 圖像 | |||||
| |||||
三角柱是一種五面體,且有一組平行面,即兩個面互相平行,而其他三個表面的法線在同一平面上(不一定是平行的面)。 這三個面可以是平行四邊形。所有平行於底面的橫截面都是相同的三角形。
由於三角柱也可以視為三面體截去2個頂點,故又稱截角三面體,另外,因為正三角柱具有對稱性,且由2種正多邊形組成,因此有人稱正三角柱為半正五面體。
一般三角柱有5個面、9個邊和6個頂點。
相關多面體與鑲嵌
編輯三角柱可以由三角形二面體的對偶三面形透過截角變換構造而來,因此與三角形二面體具有相同的對稱性,其可以衍生出一些相關的多面體:
| 對稱群:[3,2], (*322) | [3,2]+, (322) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| {3,2} |
t{3,2} |
r{3,2} |
2t{3,2}=t{2,3} | 2r{3,2}={2,3} | rr{3,2} | tr{3,2} | sr{3,2} | ||
| 半正對偶 | |||||||||
| V32 | V62 | V32 | V4.4.3 | V23 | V4.4.3 | V4.4.6 | V3.3.3.3 | ||
| 對稱群 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|
| [2n,2] [n,2] [2n,2+] |
|
|
|
|
| |||||
| 圖像 | |
|
|
|||||||
| 球面多面體 | ||||||||||
| 圖像 | |
|
|
|
||||||
| 球面鑲嵌 | 柱體 | 歐式鑲嵌 仿緊空間 |
雙曲鑲嵌 非緊空間 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| t{2,1} |
t{2,2} |
t{3,2} |
{4,2} |
t{5,2} |
t{6,2} |
t{7,2} |
t{8,2} |
... |
t{2,∞} |
t{2,iπ/λ} |
對稱性 *n32[n,3] |
球面 | 歐氏鑲嵌 | 緊湊型雙曲鑲嵌 | 仿緊型鑲嵌 | 非緊型鑲嵌 | ||||
|---|---|---|---|---|---|---|---|---|---|
| *232 [2,3] D3h |
*332 [3,3] Td |
*432 [4,3] Oh |
*532 [5,3] Ih |
*632 [6,3] P6m |
*732 [7,3] |
*832 [8,3]... |
*∞32 [∞,3] |
[iπ/λ,3] | |
| 截角頂點佈局 | 3.4.4 |
3.6.6 |
3.8.8 |
3.10.10 |
3.12.12 |
3.14.14 |
3.16.16 |
3.∞.∞ |
3.∞.∞ |
| 考克斯特紀號 施萊夫利符號 |
t{2,3} |
t{3,3} |
t{4,3} |
t{5,3} |
t{6,3} |
t{7,3} |
t{8,3} |
t{∞,3} |
t{∞,3} |
| 半正對偶圖 | |||||||||
| 三角化 頂點佈局 |
V3.4.4 |
V3.6.6 |
V3.8.8 |
V3.10.10 |
V3.12.12 |
V3.14.14 |
V3.16.16 |
V3.∞.∞ |
V3.∞.∞ |
| 考克斯特紀號 | |||||||||
| 對稱群 *n32 [n,3] |
球面鑲嵌 | 歐氏鑲嵌 | 緊湊型雙曲鑲嵌 | 仿緊型鑲嵌 | 非緊型鑲嵌 | ||||
|---|---|---|---|---|---|---|---|---|---|
| *232 [2,3] D3h |
*332 [3,3] Td |
*432 [4,3] Oh |
*532 [5,3] Ih |
*632 [6,3] P6m |
*732 [7,3] |
*832 [8,3]... |
*∞32 [∞,3] |
[iπ/λ,3] | |
| 小斜方截半 頂點佈局 |
3.4.2.4 |
3.4.3.4 |
3.4.4.4 |
3.4.5.4 |
3.4.6.4 |
3.4.7.4 |
3.4.8.4 |
3.4.∞.4 |
3.4.∞.4 |
| 考克斯特符號 施萊夫利符號 |
rr{2,3} |
rr{3,3} |
rr{4,3} |
rr{5,3} |
rr{6,3} |
rr{7,3} |
rr{8,3} |
rr{∞,3} |
rr{iπ/λ,3} |
| 鳶形 頂點佈局 |
V3.4.2.4 |
V3.4.3.4 |
V3.4.4.4 |
V3.4.5.4 |
V3.4.6.4 |
V3.4.7.4 |
V3.4.8.4 |
V3.4.∞.4 |
V3.4.∞.4 |
| 考克斯特符號 | |||||||||