三角恆等式

在數學中，三角恆等式是對出現的所有值都為實變量，涉及到三角函數的等式。這些恆等式在表達式中有些三角函數需要簡化的時候是很有用的。一個重要應用是非三角函數的積分：一個常用技巧是首先使用使用三角函數的代換規則，則通過三角恆等式可簡化結果的積分。

在幾何上依據以O為中心的單位圓可以構造角θ的很多三角函數

三角函數示意圖

幾個三角函數的圖形，分別為正弦、餘弦、正切、餘切、正割、餘割和正矢。配色與上圖相同

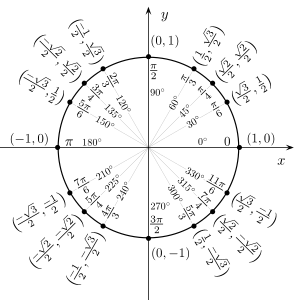單位圓的角度

符號

為了避免由於$\sin ^{-1}x$的不同意思所帶來的混淆，我們經常用下列兩個表格來表示三角函數的倒數和反函數。另外在表示餘割函數時，'$\csc$'有時會寫成比較長的'$\mathrm {cosec}$'。

函數			反函數			倒數
中文	全寫	簡寫	中文	全寫	簡寫	中文	全寫	簡寫
正弦	sine	sin	反正弦	arcsine	arcsin	餘割	cosecant	csc
餘弦	cosine	cos	反餘弦	arccosine	arccos	正割	secant	sec
正切	tangent	tan	反正切	arctangent	arctan	餘切	cotangent	cot
餘切	cotangent	cot	反餘切	arccotangent	arccot	正切	tangent	tan
正割	secant	sec	反正割	arcsecant	arcsec	餘弦	cosine	cos
餘割	cosecant	csc	反餘割	arccosecant	arccsc	正弦	sine	sin

不同的角度度量適合於不同的情況。本表展示最常用的系統。弧度是缺省的角度量並用在指數函數中。所有角度度量都是無單位的。另外在計算機中角度的符號為D，弧度的符號為R，梯度的符號為G。

相同角度的轉換表

角度單位	值								計算機中代號
轉	$0$	${\frac {1}{12}}$	${\frac {1}{8}}$	${\frac {1}{6}}$	${\frac {1}{4}}$	${\frac {1}{2}}$	${\frac {3}{4}}$	$1$	無
角度	$0^{\circ }$	$30^{\circ }$	$45^{\circ }$	$60^{\circ }$	$90^{\circ }$	$180^{\circ }$	$270^{\circ }$	$360^{\circ }$	D
弧度	$0$	${\frac {\pi }{6}}$	${\frac {\pi }{4}}$	${\frac {\pi }{3}}$	${\frac {\pi }{2}}$	$\pi$	${\frac {3\pi }{2}}$	$2\pi$	R
梯度	$0^{g}$	$33{\frac {1}{3}}^{g}$	$50^{g}$	$66{\frac {2}{3}}^{g}$	$100^{g}$	$200^{g}$	$300^{g}$	$400^{g}$	G

基本關係

三角函數間的關係，可分成正函數和餘函數

畢達哥拉斯三角恆等式如下：

$\sin ^{2}\theta +\cos ^{2}\theta =1\,$

$\tan ^{2}\theta +1\,=\sec ^{2}\theta$

$1\,+\cot ^{2}\theta =\csc ^{2}\theta$

由上面的平方關係加上三角函數的基本定義，可以導出下面的表格，即每個三角函數都可以用其他五個表達。（嚴謹地說，所有根號前都應根據實際情況添加正負號）

函數	$\sin$	$\cos$	$\tan$	$\cot$	$\sec$	$\csc$
$\sin \theta$	$\sin \theta \$	${\sqrt {1-\cos ^{2}\theta }}$	${\frac {\tan \theta }{\sqrt {1+\tan ^{2}\theta }}}$	${\frac {1}{\sqrt {1+\cot ^{2}\theta }}}$	${\frac {\sqrt {\sec ^{2}\theta -1}}{\sec \theta }}$	${\frac {1}{\csc \theta }}$
$\cos \theta$	${\sqrt {1-\sin ^{2}\theta }}$	$\cos \theta \$	${\frac {1}{\sqrt {1+\tan ^{2}\theta }}}$	${\frac {\cot \theta }{\sqrt {1+\cot ^{2}\theta }}}$	${\frac {1}{\sec \theta }}$	${\frac {\sqrt {\csc ^{2}\theta -1}}{\csc \theta }}$
$\tan \theta$	${\frac {\sin \theta }{\sqrt {1-\sin ^{2}\theta }}}$	${\frac {\sqrt {1-\cos ^{2}\theta }}{\cos \theta }}$	$\tan \theta \$	${\frac {1}{\cot \theta }}$	${\sqrt {\sec ^{2}\theta -1}}$	${\frac {1}{\sqrt {\csc ^{2}\theta -1}}}$
$\cot \theta$	${{\sqrt {1-\sin ^{2}\theta }} \over \sin \theta }$	${\cos \theta \over {\sqrt {1-\cos ^{2}\theta }}}$	${1 \over \tan \theta }$	$\cot \theta \$	${1 \over {\sqrt {\sec ^{2}\theta -1}}}$	${\sqrt {\csc ^{2}\theta -1}}$
$\sec \theta$	${1 \over {\sqrt {1-\sin ^{2}\theta }}}$	${1 \over \cos \theta }$	${\sqrt {1+\tan ^{2}\theta }}$	${{\sqrt {1+\cot ^{2}\theta }} \over \cot \theta }$	$\sec \theta \$	${\csc \theta \over {\sqrt {\csc ^{2}\theta -1}}}$
$\csc \theta$	${1 \over \sin \theta }$	${1 \over {\sqrt {1-\cos ^{2}\theta }}}$	${{\sqrt {1+\tan ^{2}\theta }} \over \tan \theta }$	${\sqrt {1+\cot ^{2}\theta }}$	${\sec \theta \over {\sqrt {\sec ^{2}\theta -1}}}$	$\csc \theta \$

其他函數的基本關係

正矢、餘矢、半正矢、半餘矢、外正割用於航行。例如半正矢可以計算球體上的兩個點之間的距離，但它們不常用。

名稱	函數	值
正矢, versine	$\operatorname {versin} \theta$ $\operatorname {vers} \theta$ $\operatorname {ver} \theta$	$1-\cos \theta$
餘的正矢, vercosine	$\operatorname {vercosin} \theta$	$1+\cos \theta$
餘矢, coversine	$\operatorname {coversin} \theta$ $\operatorname {cvs} \theta$	$1-\sin \theta$
餘的餘矢, covercosine	$\operatorname {covercosin} \theta$	$1+\sin \theta$
半正矢, haversine	$\operatorname {haversin} \theta$	${\frac {1-\cos \theta }{2}}$
餘的半正矢, havercosine	$\operatorname {havercosin} \theta$	${\frac {1+\cos \theta }{2}}$
半餘矢, hacoversine cohaversine	$\operatorname {hacoversin} \theta$	${\frac {1-\sin \theta }{2}}$
餘的半餘矢, hacovercosine cohavercosine	$\operatorname {hacovercosin} \theta$	${\frac {1+\sin \theta }{2}}$
外正割，exsecant	$\operatorname {exsec} \theta$	$\sec \theta -1$
外餘割，excosecant	$\operatorname {excsc} \theta$	$\csc \theta -1$
弦函數, chord	$\operatorname {crd} \theta$	$2\sin \left({\frac {\theta }{2}}\right)$
純虛數指數函數, cosine and imaginary unit sine	$\operatorname {cis} \theta$	$\cos \theta +i\;\sin \theta$
輻角,Argument	$\arg x$	$\operatorname {Im} (\ln x)$

對稱、移位和周期

通過檢視單位圓，可確立三角函數的下列性質，這些性質也被稱為誘導公式：

對稱

當三角函數反射自某個特定的$\theta$值，結果經常是另一個其他三角函數。這導致了下列恆等式：

反射於$\theta =0$	反射於$\theta ={\tfrac {\pi }{4}}$	反射於$\theta ={\tfrac {\pi }{2}}$	反射於$\theta ={\tfrac {3\pi }{4}}$
${\begin{aligned}\sin(0-\theta )&=-\sin \theta \\\cos(0-\theta )&=+\cos \theta \\\tan(0-\theta )&=-\tan \theta \\\cot(0-\theta )&=-\cot \theta \\\sec(0-\theta )&=+\sec \theta \\\csc(0-\theta )&=-\csc \theta \end{aligned}}$	${\begin{aligned}\sin({\tfrac {\pi }{2}}-\theta )&=+\cos \theta \\\cos({\tfrac {\pi }{2}}-\theta )&=+\sin \theta \\\tan({\tfrac {\pi }{2}}-\theta )&=+\cot \theta \\\cot({\tfrac {\pi }{2}}-\theta )&=+\tan \theta \\\sec({\tfrac {\pi }{2}}-\theta )&=+\csc \theta \\\csc({\tfrac {\pi }{2}}-\theta )&=+\sec \theta \end{aligned}}$	${\begin{aligned}\sin(\pi -\theta )&=+\sin \theta \\\cos(\pi -\theta )&=-\cos \theta \\\tan(\pi -\theta )&=-\tan \theta \\\cot(\pi -\theta )&=-\cot \theta \\\sec(\pi -\theta )&=-\sec \theta \\\csc(\pi -\theta )&=+\csc \theta \end{aligned}}$	${\begin{aligned}\sin({\tfrac {3\pi }{2}}-\theta )&=-\cos \theta \\\cos({\tfrac {3\pi }{2}}-\theta )&=-\sin \theta \\\tan({\tfrac {3\pi }{2}}-\theta )&=+\cot \theta \\\cot({\tfrac {3\pi }{2}}-\theta )&=+\tan \theta \\\sec({\tfrac {3\pi }{2}}-\theta )&=-\csc \theta \\\csc({\tfrac {3\pi }{2}}-\theta )&=-\sec \theta \end{aligned}}$

移位和周期

通過旋轉特定角度移位三角函數，經常可以找到更簡單的表達結果的不同的三角函數。例如通過旋轉${\tfrac {\pi }{2}}$、$\pi$和$2\pi$弧度移位函數。因爲這些函數的周期要麼是$\pi$要麼是$2\pi$，所以新函數和沒有移位的舊函數完全一樣。

移位${\tfrac {\pi }{2}}$	移位$\pi$	移位${\tfrac {3\pi }{2}}$	移位$2\pi$
	$\tan$和$\cot$的周期		$\sin$, $\cos$, $\csc$和$\sec$的周期
${\begin{aligned}\sin(\theta +{\tfrac {\pi }{2}})&=+\cos \theta \\\cos(\theta +{\tfrac {\pi }{2}})&=-\sin \theta \\\tan(\theta +{\tfrac {\pi }{2}})&=-\cot \theta \\\cot(\theta +{\tfrac {\pi }{2}})&=-\tan \theta \\\sec(\theta +{\tfrac {\pi }{2}})&=-\csc \theta \\\csc(\theta +{\tfrac {\pi }{2}})&=+\sec \theta \end{aligned}}$	${\begin{aligned}\sin(\theta +\pi )&=-\sin \theta \\\cos(\theta +\pi )&=-\cos \theta \\\tan(\theta +\pi )&=+\tan \theta \\\cot(\theta +\pi )&=+\cot \theta \\\sec(\theta +\pi )&=-\sec \theta \\\csc(\theta +\pi )&=-\csc \theta \end{aligned}}$	${\begin{aligned}\sin(\theta +{\tfrac {3\pi }{2}})&=-\cos \theta \\\cos(\theta +{\tfrac {3\pi }{2}})&=+\sin \theta \\\tan(\theta +{\tfrac {3\pi }{2}})&=-\cot \theta \\\cot(\theta +{\tfrac {3\pi }{2}})&=-\tan \theta \\\sec(\theta +{\tfrac {3\pi }{2}})&=+\csc \theta \\\csc(\theta +{\tfrac {3\pi }{2}})&=-\sec \theta \end{aligned}}$	${\begin{aligned}\sin(\theta +2\pi )&=+\sin \theta \\\cos(\theta +2\pi )&=+\cos \theta \\\tan(\theta +2\pi )&=+\tan \theta \\\cot(\theta +2\pi )&=+\cot \theta \\\sec(\theta +2\pi )&=+\sec \theta \\\csc(\theta +2\pi )&=+\csc \theta \end{aligned}}$

角的和差恆等式

正弦與餘弦的角和公式的圖形證明法。使用了相似三角形的性質與三角函數的定義，強調的線段是單位長度

正切的角和公式的圖形證明法。使用了相似三角形的性質與三角函數的定義，強調的線段是單位長度。

又稱做「和差定理」、「和差公式」或「和角公式」。最簡要的檢定方式是使用歐拉公式。

正弦	$\sin(\alpha \pm \beta )=\sin \alpha \cos \beta \pm \cos \alpha \sin \beta \,$
餘弦	$\cos(\alpha \pm \beta )=\cos \alpha \cos \beta \mp \sin \alpha \sin \beta \,$
正切	$\tan(\alpha \pm \beta )={\frac {\tan \alpha \pm \tan \beta }{1\mp \tan \alpha \tan \beta }}$
餘切	$\cot(\alpha \pm \beta )={\frac {\cot \alpha \cot \beta \mp 1}{\cot \beta \pm \cot \alpha }}$
正割	$\sec(\alpha \pm \beta )={\frac {\sec \alpha \sec \beta }{1\mp \tan \alpha \tan \beta }}$
餘割	$\csc(\alpha \pm \beta )={\frac {\csc \alpha \csc \beta }{\cot \beta \pm \cot \alpha }}$
注意正負號的對應。 ${\begin{aligned}x\pm y=a\pm b&\Rightarrow \ x+y=a+b\\&{\mbox{and}}\ x-y=a-b\end{aligned}}$ ${\begin{aligned}x\pm y=a\mp b&\Rightarrow \ x+y=a-b\\&{\mbox{and}}\ x-y=a+b\end{aligned}}$

正弦與餘弦的無限多項和

$\sin \left(\sum _{i=1}^{\infty }\theta _{i}\right)=\sum _{\mathrm {odd} \ k\geq 1}(-1)^{\frac {k-1}{2}}\sum _{|A|=k}\left(\prod _{i\in A}\sin \theta _{i}\prod _{i\not \in A}\cos \theta _{i}\right)$

$\cos \left(\sum _{i=1}^{\infty }\theta _{i}\right)=\sum _{\mathrm {even} \ k\geq 0}~(-1)^{\frac {k}{2}}~~\sum _{|A|=k}\left(\prod _{i\in A}\sin \theta _{i}\prod _{i\not \in A}\cos \theta _{i}\right)$

這里的"$|A|=k$"意味着索引$A$遍歷集合$\left\{1,2,3,\ldots \right\}$的大小為$k$的所有子集的集合。

在這兩個恆等式中出現了在有限多項中不出現的不對稱：在每個乘積中，只有有限多個正弦因子和餘有限多個餘弦因子。

如果只有有限多項$\theta _{i}$是非零，則在右邊只有有限多項是非零，因為正弦因子將變為零，而在每個項中，所有卻有限多的餘弦因子將是單位一。

正切的有限多項和

設$x_{i}=\tan \theta _{i}$，對於$i=1,\ldots ,n$。設$e_{k}$是變量$x_{i}$，$i=1,\ldots ,n$，$k=0,\ldots ,n$的$k$次基本對稱多項式。則

$\tan(\theta _{1}+\cdots +\theta _{n})={\frac {e_{1}-e_{3}+e_{5}-\cdots }{e_{0}-e_{2}+e_{4}-\cdots }},$

項的數目依賴於$n$。例如，

${\begin{aligned}\tan(\theta _{1}+\theta _{2}+\theta _{3})&{}={\frac {e_{1}-e_{3}}{e_{0}-e_{2}}}={\frac {(x_{1}+x_{2}+x_{3})\ -\ (x_{1}x_{2}x_{3})}{1\ -\ (x_{1}x_{2}+x_{1}x_{3}+x_{2}x_{3})}},\\\\\tan(\theta _{1}+\theta _{2}+\theta _{3}+\theta _{4})&{}={\frac {e_{1}-e_{3}}{e_{0}-e_{2}+e_{4}}}\\\\&{}={\frac {(x_{1}+x_{2}+x_{3}+x_{4})\ -\ (x_{1}x_{2}x_{3}+x_{1}x_{2}x_{4}+x_{1}x_{3}x_{4}+x_{2}x_{3}x_{4})}{1\ -\ (x_{1}x_{2}+x_{1}x_{3}+x_{1}x_{4}+x_{2}x_{3}+x_{2}x_{4}+x_{3}x_{4})\ +\ (x_{1}x_{2}x_{3}x_{4})}},\end{aligned}}$

並以此類推。一般情況可通過數學歸納法證明。

多倍角公式

$T_{n}$是$n$次切比雪夫多項式	$\cos n\theta =T_{n}\cos \theta \,$
$S_{n}$是$n$次伸展多項式	$\sin ^{2}n\theta =S_{n}\sin ^{2}\theta \,$
棣莫弗定理，$i$是虛單位	$\cos n\theta +i\sin n\theta =(\cos \theta +i\sin \theta )^{n}\,$

$1+2\cos x+2\cos 2x+2\cos 3x+\cdots +2\cos(nx)={\frac {\sin \left[\left(n+{\frac {1}{2}}\right)x\right]}{\sin {\frac {x}{2}}}}$。

（這個$x$的函數是狄利克雷核。）

雙倍角、三倍角和半角公式

這些公式可以使用和差恆等式或多倍角公式來證明。

		弦	切	割
雙倍角公式	正	${\begin{aligned}\sin 2\theta &=2\sin \theta \cos \theta \ \\&={\frac {2\tan \theta }{1+\tan ^{2}\theta }}\end{aligned}}$	${\begin{aligned}\tan 2\theta &={\frac {2\tan \theta }{1-\tan ^{2}\theta }}\ \\&={\frac {1}{1-\tan \theta }}-{\frac {1}{1+\tan \theta }}\end{aligned}}$	${\begin{aligned}\sec 2\theta &={\frac {\sec ^{2}\theta }{1-\tan ^{2}\theta }}\\&={\frac {\sec ^{2}\theta }{2-\sec ^{2}\theta }}\end{aligned}}$
	餘	${\begin{aligned}\cos 2\theta &=\cos ^{2}\theta -\sin ^{2}\theta \\&=2\cos ^{2}\theta -1\\&=1-2\sin ^{2}\theta \\&={\frac {1-\tan ^{2}\theta }{1+\tan ^{2}\theta }}\end{aligned}}$	${\begin{aligned}\cot 2\theta &={\frac {\cot ^{2}\theta -1}{2\cot \theta }}\\&={\frac {\cot \theta -\tan \theta }{2}}\end{aligned}}$	${\begin{aligned}\csc 2\theta &={\frac {\csc ^{2}\theta }{2\cot \theta }}\\&={\frac {\sec \theta \csc \theta }{2}}\end{aligned}}$
降次公式	正	$\sin ^{2}\theta ={\frac {1-\cos 2\theta }{2}}$	$\tan ^{2}\theta ={\frac {1-\cos 2\theta }{1+\cos 2\theta }}$
	餘	$\cos ^{2}\theta ={\frac {1+\cos 2\theta }{2}}$	$\cot ^{2}\theta ={\frac {1+\cos 2\theta }{1-\cos 2\theta }}$
三倍角公式	正	${\begin{aligned}\sin 3\theta &=3\sin \theta -4\sin ^{3}\theta \\&=4\sin \theta \sin \left({\frac {\pi }{3}}-\theta \right)\sin \left({\frac {\pi }{3}}+\theta \right)\end{aligned}}$	${\begin{aligned}\tan 3\theta &={\frac {3\tan \theta -\tan ^{3}\theta }{1-3\tan ^{2}\theta }}\\&=\tan \theta \tan \left({\frac {\pi }{3}}-\theta \right)\tan \left({\frac {\pi }{3}}+\theta \right)\end{aligned}}$	${\begin{aligned}\sec 3\theta &={\frac {\sec ^{3}\theta }{4-3\sec ^{2}\theta }}\\&={\dfrac {1}{4\cos \theta \cos \left({\dfrac {\pi }{3}}-\theta \right)\cos \left({\dfrac {\pi }{3}}+\theta \right)}}\end{aligned}}$
	餘	${\begin{aligned}\cos 3\theta &=4\cos ^{3}\theta -3\cos \theta \\&=4\cos \theta \cos \left({\frac {\pi }{3}}-\theta \right)\cos \left({\frac {\pi }{3}}+\theta \right)\end{aligned}}$	${\begin{aligned}\cot 3\theta &={\frac {\cot ^{3}\theta -3\cot \theta }{3\cot ^{2}\theta -1}}\\&=\cot \theta \cot \left({\frac {\pi }{3}}-\theta \right)\cot \left({\frac {\pi }{3}}+\theta \right)\end{aligned}}$	${\begin{aligned}\csc 3\theta &={\frac {\csc ^{3}\theta }{3\csc ^{2}\theta -4}}\\&={\dfrac {1}{4\sin \theta \sin \left({\dfrac {\pi }{3}}-\theta \right)\sin \left({\dfrac {\pi }{3}}+\theta \right)}}\end{aligned}}$
半角公式	正	$\sin {\frac {\theta }{2}}=\pm \,{\sqrt {\frac {1-\cos \theta }{2}}}$	${\begin{aligned}\tan {\frac {\theta }{2}}&=\csc \theta -\cot \theta \\&=\pm \,{\sqrt {1-\cos \theta \over 1+\cos \theta }}\\&={\frac {\sin \theta }{1+\cos \theta }}\\&={\frac {1-\cos \theta }{\sin \theta }}\\&={\frac {\cos \theta +\sin \theta -1}{\cos \theta -\sin \theta +1}}\\&={\sqrt {\cot ^{2}\theta +1}}-\cot \theta \end{aligned}}$	$\sec {\frac {\theta }{2}}=\pm \,{\sqrt {\frac {2\sec \theta }{\sec \theta +1}}}$
	餘	$\cos {\frac {\theta }{2}}=\pm \,{\sqrt {\frac {1+\cos \theta }{2}}}$	${\begin{aligned}\cot {\frac {\theta }{2}}&=\csc \theta +\cot \theta \\&=\pm \,{\sqrt {1+\cos \theta \over 1-\cos \theta }}\\&={\frac {\sin \theta }{1-\cos \theta }}\\&={\frac {1+\cos \theta }{\sin \theta }}\\&={\frac {\cos \theta -\sin \theta +1}{\cos \theta +\sin \theta -1}}\\&={\sqrt {\cot ^{2}\theta +1}}+\cot \theta \end{aligned}}$	$\csc {\frac {\theta }{2}}=\pm \,{\sqrt {\frac {2\sec \theta }{\sec \theta -1}}}$

n倍角公式

$n$倍角公式
$\sin n\theta =\sum _{k=0}^{n}{\binom {n}{k}}\cos ^{k}\theta \,\sin ^{n-k}\theta \,\sin \left[{\frac {1}{2}}(n-k)\pi \right]=\sin \theta \sum _{k=0}^{\lfloor {\frac {n-1}{2}}\rfloor }(-1)^{k}{\binom {n-1-k}{k}}~(2\cos \theta )^{n-1-2k}$ （第二類切比雪夫多項式）
$\cos n\theta =\sum _{k=0}^{n}{\binom {n}{k}}\cos ^{k}\theta \,\sin ^{n-k}\theta \,\cos \left[{\frac {1}{2}}(n-k)\pi \right]={\frac {1}{2}}\sum _{k=0}^{\lfloor {\frac {n}{2}}\rfloor }(-1)^{k}{\frac {n}{n-k}}{\binom {n-k}{k}}~(2\cos \theta )^{n-2k}$ （第一類切比雪夫多項式）
$\tan n\theta ={\frac {\displaystyle \sum _{k=1}^{\left[{\frac {n}{2}}\right]}(-1)^{k+1}{\binom {n}{2k-1}}\tan ^{2k-1}\theta }{\displaystyle \sum _{k=1}^{\left[{\frac {n+1}{2}}\right]}(-1)^{k+1}{\binom {n}{2(k-1)}}\tan ^{2(k-1)}\theta }}$
$n$倍遞迴公式
$\tan \,n\theta ={\frac {\tan(n{-}1)\theta +\tan \theta }{1-\tan(n{-}1)\theta \,\tan \theta }}$、$\cot \,n\theta ={\frac {\cot(n{-}1)\theta \,\cot \theta -1}{\cot(n{-}1)\theta +\cot \theta }}$。(遞迴關係)

參見正切半角公式，它也叫做「萬能公式」。

其他函數的倍半角公式

正矢

• $\operatorname {versin} 2\theta =2\sin ^{2}\theta ={\frac {(\sin 2\theta )(\sin \theta )}{\cos \theta }}=1-\cos 2\theta$

餘矢

• $\operatorname {cvs} 2\theta =(\sin \theta -\cos \theta )^{2}=1-\sin 2\theta$

冪簡約公式

從解餘弦二倍角公式的第二和第三版本得到。

正弦	餘弦	其他
$\sin ^{2}\theta ={\frac {1-\cos 2\theta }{2}}$	$\cos ^{2}\theta ={\frac {1+\cos 2\theta }{2}}$	$\sin ^{2}\theta \cos ^{2}\theta ={\frac {1-\cos 4\theta }{8}}$
$\sin ^{3}\theta ={\frac {3\sin \theta -\sin 3\theta }{4}}$	$\cos ^{3}\theta ={\frac {3\cos \theta +\cos 3\theta }{4}}$	$\sin ^{3}\theta \cos ^{3}\theta ={\frac {3\sin 2\theta -\sin 6\theta }{32}}$
$\sin ^{4}\theta ={\frac {3-4\cos 2\theta +\cos 4\theta }{8}}$	$\cos ^{4}\theta ={\frac {3+4\cos 2\theta +\cos 4\theta }{8}}$	$\sin ^{4}\theta \cos ^{4}\theta ={\frac {3-4\cos 4\theta +\cos 8\theta }{128}}$
$\sin ^{5}\theta ={\frac {10\sin \theta -5\sin 3\theta +\sin 5\theta }{16}}$	$\cos ^{5}\theta ={\frac {10\cos \theta +5\cos 3\theta +\cos 5\theta }{16}}$	$\sin ^{5}\theta \cos ^{5}\theta ={\frac {10\sin 2\theta -5\sin 6\theta +\sin 10\theta }{512}}$

	餘弦	正弦
如果$n$是奇數	$\cos ^{n}\theta ={\frac {2}{2^{n}}}\sum _{k=0}^{\frac {n-1}{2}}{\binom {n}{k}}\cos {[(n-2k)\theta ]}$	$\sin ^{n}\theta ={\frac {2}{2^{n}}}\sum _{k=0}^{\frac {n-1}{2}}(-1)^{\left({\frac {n-1}{2}}-k\right)}{\binom {n}{k}}\sin {[(n-2k)\theta ]}$
如果$n$是偶數	$\cos ^{n}\theta ={\frac {1}{2^{n}}}{\binom {n}{\frac {n}{2}}}+{\frac {2}{2^{n}}}\sum _{k=0}^{{\frac {n}{2}}-1}{\binom {n}{k}}\cos {[(n-2k)\theta ]}$	$\sin ^{n}\theta ={\frac {1}{2^{n}}}{\binom {n}{\frac {n}{2}}}+{\frac {2}{2^{n}}}\sum _{k=0}^{{\frac {n}{2}}-1}(-1)^{\left({\frac {n}{2}}-k\right)}{\binom {n}{k}}\cos {[(n-2k)\theta ]}$

數值連乘

$\prod _{k=0}^{n-1}\cos 2^{k}\theta ={\frac {\sin 2^{n}\theta }{2^{n}\sin \theta }}$

$\prod _{k=0}^{n-1}\sin \left(x+{\frac {k\pi }{n}}\right)={\frac {\sin nx}{2^{n-1}}}$

$\prod _{k=1}^{n-1}\sin \left({\frac {k\pi }{n}}\right)={\frac {n}{2^{n-1}}}$,$\prod _{k=1}^{n-1}\sin \left({\frac {k\pi }{2n}}\right)={\frac {\sqrt {n}}{2^{n-1}}}$,$\prod _{k=1}^{n}\sin \left({\frac {k\pi }{2n+1}}\right)={\frac {\sqrt {2n+1}}{2^{n}}}$

$\prod _{k=1}^{n-1}\cos \left({\frac {k\pi }{n}}\right)={\frac {\sin {\frac {n\pi }{2}}}{2^{n-1}}}$,$\prod _{k=1}^{n-1}\cos \left({\frac {k\pi }{2n}}\right)={\frac {\sqrt {n}}{2^{n-1}}}$,$\prod _{k=1}^{n}\cos \left({\frac {k\pi }{2n+1}}\right)={\frac {1}{2^{n}}}$

$\prod _{k=1}^{n-1}\tan \left({\frac {k\pi }{n}}\right)={\frac {n}{\sin {\frac {n\pi }{2}}}}$,$\prod _{k=1}^{n-1}\tan \left({\frac {k\pi }{2n}}\right)=1$,$\prod _{k=1}^{n}\tan {\frac {k\pi }{2n+1}}={\sqrt {2n+1}}$

常見的恆等式

積化和差與和差化積恆等式

數學家韋達在其三角學著作《應用於三角形的數學定律》給出積化和差與和差化積恆等式。積化和差恆等式可以通過展開角的和差恆等式的右手端來證明。

積化和差	和差化積
$\sin \alpha \cos \beta ={\sin(\alpha +\beta )+\sin(\alpha -\beta ) \over 2}$	$\sin \alpha +\sin \beta =2\sin {\frac {\alpha +\beta }{2}}\cos {\frac {\alpha -\beta }{2}}$
$\cos \alpha \sin \beta ={\sin(\alpha +\beta )-\sin(\alpha -\beta ) \over 2}$	$\sin \alpha -\sin \beta =2\cos {\alpha +\beta \over 2}\sin {\alpha -\beta \over 2}$
$\cos \alpha \cos \beta ={\cos(\alpha +\beta )+\cos(\alpha -\beta ) \over 2}$	$\cos \alpha +\cos \beta =2\cos {\frac {\alpha +\beta }{2}}\cos {\frac {\alpha -\beta }{2}}$
$\sin \alpha \sin \beta =-{\cos(\alpha +\beta )-\cos(\alpha -\beta ) \over 2}$	$\cos \alpha -\cos \beta =-2\sin {\alpha +\beta \over 2}\sin {\alpha -\beta \over 2}$

平方差公式

$\sin(x+y)\sin(x-y)=\sin ^{2}{x}-\sin ^{2}{y}=\cos ^{2}{y}-\cos ^{2}{x}\,$

$\cos(x+y)\cos(x-y)=\cos ^{2}{x}-\sin ^{2}{y}=\cos ^{2}{y}-\sin ^{2}{x}\,$

(可藉由積化和差公式+2倍角公式推導而來)

其他恆等式

如果$x+y+z=n\pi$，

那麼$\tan x+\tan y+\tan z=\tan x\tan y\tan z$

$\cot x\cot y+\cot y\cot z+\cot z\cot x=1$

如果$x+y+z=n\pi +{\frac {\pi }{2}}$，

那麼$\tan x\tan y+\tan y\tan z+\tan z\tan x=1$

$\cot x+\cot y+\cot z=\cot x\cot y\cot z$

如果$x+y+z=\pi$，

那麼$\sin 2x+\sin 2y+\sin 2z=4\sin x\sin y\sin z$

$\sin x+\sin y+\sin z=4\cos {\frac {x}{2}}\cos {\frac {y}{2}}\cos {\frac {z}{2}}$

$\cos x+\cos y+\cos z=1+4\sin {\frac {x}{2}}\sin {\frac {y}{2}}\sin {\frac {z}{2}}$

托勒密定理

如果$w+x+y+z=\pi$（半圓）

那麼:

${\begin{aligned}\sin(w+x)\sin(x+y)&=\sin(x+y)\sin(y+z)\\&=\sin(y+z)\sin(z+w)\\&{}=\sin(z+w)\sin(w+x)\\&{}=\sin w\sin y+\sin x\sin z\end{aligned}}$

（前三個等式是一般情況；第四個是本質。）

三角函數與雙曲函數的恆等式

利用三角恆等式的指數定義和雙曲函數的指數定義即可求出下列恆等式：

$e^{ix}=\cos x+i\;\sin x,\;e^{-ix}=\cos x-i\;\sin x$

$e^{x}=\cosh x+\sinh x\!,\;e^{-x}=\cosh x-\sinh x\!$

所以

$\cosh ix={\tfrac {1}{2}}(e^{ix}+e^{-ix})=\cos x$

$\sinh ix={\tfrac {1}{2}}(e^{ix}-e^{-ix})=i\sin x$

下表列出部分的三角函數與雙曲函數的恆等式：

三角函數	雙曲函數
$\sin \theta =-i\sinh {i\theta }\,$	$\sinh {\theta }=i\sin {(-i\theta )}\,$
$\cos {\theta }=\cosh {i\theta }\,$	$\cosh {\theta }=\cos {(-i\theta )}\,$
$\tan \theta =-i\tanh {i\theta }\,$	$\tanh {\theta }=i\tan {(-i\theta )}\,$
$\cot {\theta }=i\coth {i\theta }\,$	$\coth \theta =-i\cot {(-i\theta )}\,$
$\sec {\theta }=\operatorname {sech} {\,i\theta }\,$	$\operatorname {sech} {\theta }=\sec {(-i\theta )}\,$
$\csc {\theta }=i\;\operatorname {csch} {\,i\theta }\,$	$\operatorname {csch} \theta =-i\csc {(-i\theta )}\,$

• 其他恆等式：

$\cosh ix={\tfrac {1}{2}}(e^{ix}+e^{-ix})=\cos x$

$\sinh ix={\tfrac {1}{2}}(e^{ix}-e^{-ix})=i\sin x$

$\cosh(x+iy)=\cosh(x)\cos(y)+i\sinh(x)\sin(y)\,$

$\sinh(x+iy)=\sinh(x)\cos(y)+i\cosh(x)\sin(y)\,$

$\tanh ix=i\tan x\,$

$\cosh x=\cos ix\,$

$\sinh x=-i\sin ix\,$

$\tanh x=-i\tan ix\,$

線性組合

對於某些用途，知道同樣周期但不同相位移動的正弦波的任何線性組合是有相同周期但不同相位移動的正弦波是重要的。在正弦和餘弦波的線性組合的情況下，我們有

$a\sin x+b\cos x={\sqrt {a^{2}+b^{2}}}\cdot \sin(x+\varphi )\;(a>0)$

這裏的

$\varphi =\arctan \left({\frac {b}{a}}\right)$

這個公式也叫輔助角公式或李善蘭公式。更一般的說，對於任何相位移動，我們有

$a\sin x+b\sin(x+\alpha )=c\sin(x+\beta )\;(a+b\cos x>0)$

這裏

$c={\sqrt {a^{2}+b^{2}+2ab\cos \alpha }},$

而

$\beta =\arctan \left({\frac {b\sin \alpha }{a+b\cos \alpha }}\right)$

反三角函數

主條目：反三角函數

$\arcsin x+\arccos x={\frac {\pi }{2}}\;$

$\arctan x+\operatorname {arccot} x={\frac {\pi }{2}}.\;$

$\arctan x+\arctan {\frac {1}{x}}=\left\{{\begin{matrix}{\frac {\pi }{2}},&{\mbox{if }}x>0\\-{\frac {\pi }{2}},&{\mbox{if }}x<0\end{matrix}}\right.$

$\arctan x+\arctan y=\arctan {\frac {x+y}{1-xy}}+\left\{{\begin{matrix}\pi ,&{\mbox{if }}x,y>0\\-\pi ,&{\mbox{if }}x,y<0\\0,&{\mbox{otherwise }}\end{matrix}}\right.$

$\sin(\arccos x)={\sqrt {1-x^{2}}}\,$

$\sin(\arctan x)={\frac {x}{\sqrt {1+x^{2}}}}$

$\cos(\arctan x)={\frac {1}{\sqrt {1+x^{2}}}}$

$\cos(\arcsin x)={\sqrt {1-x^{2}}}\,$

$\tan(\arcsin x)={\frac {x}{\sqrt {1-x^{2}}}}$

$\tan(\arccos x)={\frac {\sqrt {1-x^{2}}}{x}}$

無限乘積公式

為了用於特殊函數，有下列三角函數無窮乘積公式：

$\sin x=x\prod _{n=1}^{\infty }\left(1-{\frac {x^{2}}{\pi ^{2}n^{2}}}\right)$

$\sinh x=x\prod _{n=1}^{\infty }\left(1+{\frac {x^{2}}{\pi ^{2}n^{2}}}\right)$

${\frac {\sin x}{x}}=\prod _{n=1}^{\infty }\cos \left({\frac {x}{2^{n}}}\right)$

$\cos x=x\prod _{n=1}^{\infty }\left(1-{\frac {x^{2}}{\pi ^{2}(n-{\frac {1}{2}})^{2}}}\right)$

$\cosh x=\prod _{n=1}^{\infty }\left(1+{\frac {x^{2}}{\pi ^{2}(n-{\frac {1}{2}})^{2}}}\right)$

$|\sin x|={\frac {1}{2}}\prod _{n=0}^{\infty }{\sqrt[{2^{n+1}}]{\left|\tan \left(2^{n}x\right)\right|}}$

微積分

正弦的微分

正弦（藍色）、正弦的微分（橘色），其中，正弦的微分正好是餘弦。

餘弦的微分

餘弦（藍色）、餘弦的微分（橘色），其中，餘弦的微分正好是正弦的對x軸的鏡射。

在微積分中，下面陳述的關係要求角用弧度來度量；如果用其他方式比如角度來這些關係會變得更加複雜。如果三角函數以幾何的方式來定義，它們的導數可以通過驗證兩個極限而找到。第一個是：

$\lim _{x\rightarrow 0}{\frac {\sin x}{x}}=1$

可以使用單位圓和夾擠定理來驗證。如果用洛必達法則來證明這個極限，那也就用這個極限證明了正弦的導數是餘弦，並因此在應用洛必達法則中使用正弦的導數是餘弦的事實，就是邏輯謬論中的循環論證了。第二個極限是：

$\lim _{x\rightarrow 0}{\frac {\cos x-1}{x}}=0$

使用恆等式$\tan {\frac {x}{2}}=1-{\frac {\cos x}{\sin x}}$驗證。已經確立了這兩個極限，你可以使用導數的極限定義和加法定理來證明$\sin 'x=\cos x$和$\cos 'x=-\sin x$。如果正弦和餘弦函數用它們的泰勒級數來定義，則導數可以通過冪級數逐項微分得到。

${d \over dx}\sin(x)=\cos(x)$

結果的三角函數可以使用上述恆等式和微分規則來做微分。

${\begin{aligned}{d \over dx}\sin x&=\cos x,&{d \over dx}\arcsin x&={1 \over {\sqrt {1-x^{2}}}}\\\\{d \over dx}\cos x&=-\sin x,&{d \over dx}\arccos x&=-{1 \over {\sqrt {1-x^{2}}}}\\\\{d \over dx}\tan x&=\sec ^{2}x,&{d \over dx}\arctan x&={1 \over 1+x^{2}}\\\\{d \over dx}\cot x&=-\csc ^{2}x,&{d \over dx}\operatorname {arccot} x&=-{1 \over 1+x^{2}}\\\\{d \over dx}\sec x&=\tan x\sec x,&{d \over dx}\operatorname {arcsec} x&={1 \over |x|{\sqrt {x^{2}-1}}}\\\\{d \over dx}\csc x&=-\csc x\cot x,&{d \over dx}\operatorname {arccsc} x&=-{1 \over |x|{\sqrt {x^{2}-1}}}\end{aligned}}$

在三角函數積分表中可以找到積分恆等式。

蘊涵

三角函數（正弦和餘弦）的微分是同樣兩個函數線性組合的事實在很多數學領域包括微分方程和傅立葉變換中是重要的基本原理。

指數定義

函數	反函數
$\sin \theta ={\frac {e^{{i}\theta }-e^{-{i}\theta }}{2{i}}}\,$	$\arcsin x=-{i}\ln \left({i}x+{\sqrt {1-x^{2}}}\right)\,$
$\cos \theta ={\frac {e^{{i}\theta }+e^{-{i}\theta }}{2}}\,$	$\arccos x=-{i}\ln \left(x+{\sqrt {x^{2}-1}}\right)\,$
$\tan \theta ={\frac {e^{{i}\theta }-e^{-{i}\theta }}{{i}(e^{{i}\theta }+e^{-{i}\theta })}}\,$	$\arctan x={\frac {i}{2}}\ln \left({\frac {{i}+x}{{i}-x}}\right)\,$
$\csc \theta ={\frac {2{i}}{e^{{i}\theta }-e^{-{i}\theta }}}\,$	$\operatorname {arccsc} x=-{i}\ln \left({\tfrac {i}{x}}+{\sqrt {1-{\tfrac {1}{x^{2}}}}}\right)\,$
$\sec \theta ={\frac {2}{e^{{i}\theta }+e^{-{i}\theta }}}\,$	$\operatorname {arcsec} x=-{i}\ln \left({\tfrac {1}{x}}+{\sqrt {1-{\tfrac {i}{x^{2}}}}}\right)\,$
$\cot \theta ={\frac {{i}(e^{{i}\theta }+e^{-{i}\theta })}{e^{{i}\theta }-e^{-{i}\theta }}}\,$	$\operatorname {arccot} x={\frac {i}{2}}\ln \left({\frac {{i}-x}{{i}+x}}\right)\,$
$\operatorname {cis} \,\theta =e^{{i}\theta }\,$	$\operatorname {arccis} \,x=-{i}\ln x\,$
$\sinh \theta ={\frac {e^{\theta }-e^{-\theta }}{2}}\,$	$\operatorname {arcsinh} \,x=\ln \left(x\pm {\sqrt {x^{2}+1}}\right)\,$
$\cosh \theta ={\frac {e^{\theta }+e^{-\theta }}{2}}\,$	$\operatorname {arccosh} \,x=\ln \left(x\pm {\sqrt {x^{2}-1}}\right)=\pm \ln \left(x+{\sqrt {x^{2}-1}}\right)\,$
$\tanh \theta ={\frac {\sinh \theta }{\cosh \theta }}={\frac {e^{\theta }-e^{-\theta }}{e^{\theta }+e^{-\theta }}}\,$	$\operatorname {arctanh} \,x={\frac {1}{2}}\ln \left({\frac {1+x}{1-x}}\right)\,$

參見

• 餘弦定理
• 三角函數
• 正弦定理
• 正切定理
• 中線長公式
• 角平分線長公式
• 雙曲函數恆等式
• 三分之一角公式

參考文獻

來源

• A one-page proof of many trigonometric identities using Euler's formula，by Connelly Barnes.
• Useful Formulae for Hong Kong Advanced Level Examination Pure Mathematics.