β-二項式分佈

Β-二項式分佈，或稱貝塔-二項式分佈，是機率論與統計學中的有限空間取值的一類離散型機率分佈函數。它與一般二項式分佈的不同之處，在於它雖然也是表示一系列已知次數的伯努利實驗的成功機率，但其中的伯努利實驗的常數變成了一個隨機變量。作為過度散佈的二項式分佈，Β-二項式分佈在貝氏統計、經驗貝葉斯方法以及經典統計學中都常常用到。

Β-二項式分佈

機率質量函數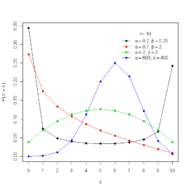
累積分佈函數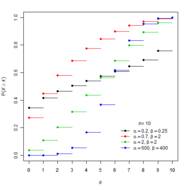
參數	n ∈ N0 —試驗次數 $\alpha >0$ （實數） $\beta >0$ （實數）
值域	k ∈ { 0, …, n }
機率質量函數	${n \choose k}{\frac {\mathrm {B} (k+\alpha ,n-k+\beta )}{\mathrm {B} (\alpha ,\beta )}}\!$
累積分佈函數	$1-{\tfrac {\mathrm {B} (\beta +n-k-1,\alpha +k+1)_{3}F_{2}({\boldsymbol {a}},{\boldsymbol {b}};k)}{\mathrm {B} (\alpha ,\beta )\mathrm {B} (n-k,k+2)(n+1)}}$ ，其中 3F2(a,b,k)=3F2(1,α+k+1, -n+k+1,k+2, -β-n+k +2,1) 是廣義超幾何分佈
期望值	${\frac {n\alpha }{\alpha +\beta }}\!$
變異數	${\frac {n\alpha \beta (\alpha +\beta +n)}{(\alpha +\beta )^{2}(\alpha +\beta +1)}}\!$
偏度	${\tfrac {(\alpha +\beta +2n)(\beta -\alpha )}{(\alpha +\beta +2)}}{\sqrt {\tfrac {1+\alpha +\beta }{n\alpha \beta (n+\alpha +\beta )}}}\!$
動差母函數	$_{2}F_{1}(-n,\alpha ;\alpha +\beta ;1-e^{t})\!$ ${\text{for }}t<\log _{e}(2)$
特徵函數	$_{2}F_{1}(-n,\alpha ;\alpha +\beta ;1-e^{it})\!$ ${\text{for }}|t|<\log _{e}(2)$

當試驗次數 n = 1 的時候，Β-二項式分佈退化為伯努利分佈，而在α = β = 1 的時候，Β-二項式分佈則退化為取值從0 到 n 的離散型均勻分佈。當 α 和 β 足夠大的時候，它能夠任意逼近二項式分佈。Β-二項式分佈也是多變量波利亞分佈在一元時的情況，正如二項式分佈和Β分佈分別是多項分佈和狄利克雷分佈在一元時的情況一樣。

矩相關性質

Β-二項式分佈的前三個矩分別是：

${\begin{aligned}\mu _{1}&={\frac {n\alpha }{\alpha +\beta }}\\[8pt]\mu _{2}&={\frac {n\alpha [n(1+\alpha )+\beta ]}{(\alpha +\beta )(1+\alpha +\beta )}}\\[8pt]\mu _{3}&={\frac {n\alpha [n^{2}(1+\alpha )(2+\alpha )+3n(1+\alpha )\beta +\beta (\beta -\alpha )]}{(\alpha +\beta )(1+\alpha +\beta )(2+\alpha +\beta )}}\end{aligned}}$

而峰度則是：

$\gamma _{2}={\frac {(\alpha +\beta )^{2}(1+\alpha +\beta )}{n\alpha \beta (\alpha +\beta +2)(\alpha +\beta +3)(\alpha +\beta +n)}}\left[(\alpha +\beta )(\alpha +\beta -1+6n)+3\alpha \beta (n-2)+6n^{2}-{\frac {3\alpha \beta n(6-n)}{\alpha +\beta }}-{\frac {18\alpha \beta n^{2}}{(\alpha +\beta )^{2}}}\right].$

設 $\pi ={\frac {\alpha }{\alpha +\beta }}\!$ 那麼數學期望值可以表示成

$\mu ={\frac {n\alpha }{\alpha +\beta }}=n\pi \!$

而方差則是：

$\sigma ^{2}={\frac {n\alpha \beta (\alpha +\beta +n)}{(\alpha +\beta )^{2}(\alpha +\beta +1)}}=n\pi (1-\pi ){\frac {\alpha +\beta +n}{\alpha +\beta +1}}=n\pi (1-\pi )[1+(n-1)\rho ]\!$

其中 $\rho ={\tfrac {1}{\alpha +\beta +1}}\!$ 是 n 個伯努利變量的關聯繫數，稱為散佈系數。

參見

• 多變量波利亞分佈

參考來源

• Minka, Thomas P. (2003). Estimating a Dirichlet distribution （頁面存檔備份，存於互聯網檔案館）. Microsoft Technical Report.

外部連結

• 使用Β-二項式分佈來對生物識別設備的性能作出估計 （頁面存檔備份，存於互聯網檔案館）