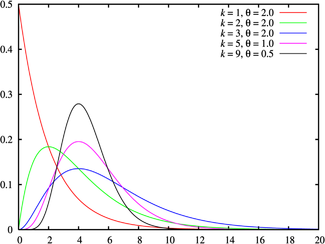
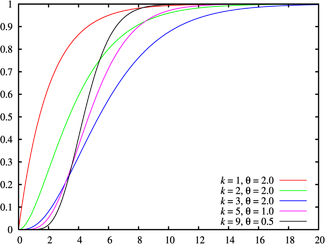
假設X1, X2, ... Xn 為連續發生事件的等候時間,且這n次等候時間為獨立的,那麼這n次等候時間之和Y (Y=X1+X2+...+Xn)服從伽瑪分佈,即 Y~Gamma(α , β),亦可記作Y~Gamma(α , λ),其中α = n,而 β 與λ互為倒數關係,λ 表單位時間內事件的發生率。
指數分佈為α = 1的伽瑪分佈。
有兩種表記方法:
或
兩者所表達意義相同,只要將以下式子做 的替換即可,即,其機率密度函數為:
,x > 0
其中Gamma函數之特徵為:
-
-
-
-
當兩隨機變量服從Gamma分佈,且相互獨立,且參數( 或 )相同時,Gamma分佈具有可加性。
-