累積分布函數

累積分布函數（英語：cumulative distribution function，CDF）或機率分布函數，簡稱分布函數，是機率密度函數的積分，能完整描述一個實隨機變數$X$的機率分布。

指數分布的累積分布函數

常態分布的累積分布函數

在標量連續分布的情況下，它給出了從負無窮到$x$的機率密度函數下的面積。 累積分布函數也用於指定多元隨機變數的分布。

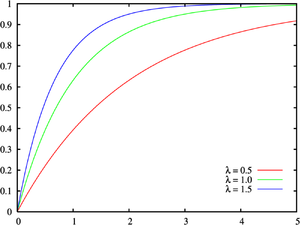
定義

對於所有實數值的隨機變數$X$ ，累積分布函數定義如下：

$$F_{X}(x)=\operatorname {P} (X\leq x)$$

Eq.1

其中右側表示隨機變數$X$取值小於或等於$x$的機率。

對於$X$位於半閉區間$(a,b]$ 的機率，其中$a<b$，因此定義是:

$$\operatorname {P} (a<X\leq b)=F_{X}(b)-F_{X}(a)$$

Eq.2

在上面的定義中，「小於或等於」符號「≤」是一種約定，不是普遍使用的（例如匈牙利文獻使用「<」），但這種區別對於離散分布很重要。二項式分布和卜瓦松分布的表格的正確使用取決於此約定。此外，像數學家保羅·皮埃爾·萊維(Paul Lévy)的特徵函數反演公式等重要公式也依賴於「小於或等於」公式。

性質

• 有界性
  • $\lim _{x\to -\infty }F_{X}(x)=0$
  • $\lim _{x\to +\infty }F_{X}(x)=1$
• 單調性：
  • $F_{X}(x_{1})\leq F_{X}(x_{2}),\ {\mbox{if}}\,x_{1}<x_{2}$
• 右連續性：
  • $\lim _{x\rightarrow x_{0}^{+}}F_{X}(x)=F_{X}(x_{0})$

$X$之值落在一區間$(a,b]$之內的機率為

$\operatorname {P} (a<X\leq b)=F_{X}(b)-F_{X}(a)$

一隨機變數$X$的CDF與其PDF的關係為

$F_{X}(x)=\int _{-\infty }^{x}f_{X}(t)\,dt$

反函數

若累積分布函數 $F$ 是連續的嚴格增函數，則存在其反函數$F^{-1}(y),y\in [0,1]$。累積分布函數的反函數可以用來生成服從該隨機分布的隨機變數。設若$F_{X}(x)$是機率分布$X$的累積分布函數，並存在反函數$F_{X}^{-1}$。若$a$是$[0,1)$區間上均勻分布的隨機變數，則$F_{X}^{-1}(a)$服從$X$分布。

互補累積分布函數

互補累積分布函數（complementary cumulative distribution function、CCDF），是對連續函數，所有大於$a$的值，其出現機率的和。

$F(a)=P(x>a)$

參見

• 機率密度函數
• 機率質量函數