最大流问题

在优化理论中，最大流问题（英语：Maximum flow problem）涉及到在一个单源点、单汇点的网络流中找到一条最大的流。

一个网络最大流的例子。源点为 s，汇点为 t。数字表示流和容量。

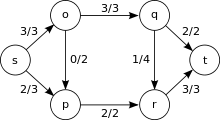
最大流问题可以被看作是一个更复杂的网络流问题（循环问题，circulation problem）的特殊情况。s-t流（从源点s到汇点t）的最大值等于s-t割的最小容量，这被称为最大流最小割定理。

历史

最大流问题最早是在1954年由泰德·哈里斯和F·S·罗斯（F. S. Ross）通过一个苏联铁路的交通流量的简化模型提出的。 1955年，小莱斯特·伦道夫·福特和德尔伯特·雷·富尔克森创建了第一个已知的算法，福特-富尔克森算法。

多年来，最大流问题的各种改进算法被发现，例如杰克·埃德蒙兹、理查德·卡普和叶菲姆·迪尼茨的最短增广路算法；迪尼茨的阻塞流算法；安德鲁·V·戈德堡和罗伯特·塔扬的Push-Relabel算法；戈德堡和Rao的binary阻塞流算法；Christiano、Kelner和亚历山大·马德瑞（Aleksander Madry）的电流算法；Spielman发现一个最大流近似最优解，但仅适用于无向图。

定义

一个网络流，源点为 s，汇点为 t。边上的数字为容量。

设$N=(V,E)$为一个网络，其中$s$和$t$分别是$N$的源点和汇点（$s,t\in V$）。

一个边的容量为映射$c:E\to \mathbb {R} ^{+}$，记为$c_{uv}$或$c(u,v)$。它表示可以通过一条边的流量的最大值。

一个流为一个映射$f:E\to \mathbb {R} ^{+}$，记为$f_{uv}$或$f(u,v)$，遵循下面两个限制：

1. 对于每个$(u,v)\in E$，有$f_{uv}\leq c_{uv}$（即容量限制：一个边的流量不能超过它的容量）；
2. 对于每个$v\in V\setminus \{s,t\}$，有$\sum _{u:(u,v)\in E}f_{uv}=\sum _{u:(v,u)\in E}f_{vu}$（即流的保留：流入一个节点的流的总和必须等于流出这个节点的流的总和，源点和汇点除外）。

流量定义为 $|f|=\sum _{v:(s,v)\in E}f_{sv}$，其中$s$为$N$的源点，它表示从源点到汇点的流的数量。

最大流问题就是最大化$|f|$，即从$s$点到$t$点尽可能规划最大的流量。

解法

算法	复杂度	描述
线性规划
福特-富尔克森算法	O(E max| f |)
埃德蒙兹-卡普算法	O(VE2)	福特-富尔克森算法的特例，使用广度优先搜索寻找增广路径.
迪尼茨阻塞流算法	O(V2E)
MPM (Malhotra, Pramodh-Kumar and Maheshwari)算法	O(V3)	只适用于无环图。参考 Original Paper.
Dinic算法	O(VE log(V))
push-relabel maximum flow算法	O(V2E)
Push-relabel算法，使用FIFO vertex selection rule	O(V3)
Push-relabel算法，使用 dynamic trees	$O\left(VE\log {\frac {V^{2}}{E}}\right)$
KRT (King, Rao, Tarjan)算法	$O(EV\log _{\frac {E}{V\log V}}V)$
Binary阻塞流算法	$O\left(E\cdot \min(V^{\frac {2}{3}},{\sqrt {E}})\cdot \log {\frac {V^{2}}{E}}\log {U}\right)$
James B Orlin's + KRT (King, Rao, Tarjan)算法	$O(VE)$	Orlin's algorithm （页面存档备份，存于互联网档案馆） solves max-flow in O(VE) time for $E\leq O(V^{{16 \over 15}-\epsilon })$ while KRT solves it in O(VE) for $E>V^{1+\epsilon }$.