恒星视差
恒星视差是天文学中因为恒星距离产生视差的效应。它是恒星际尺度的视差,经由天文测量学,视差可以直接测量出一颗恒星与地球的准确距离。它曾是天文学辩论了数百年的议题,但是因为太困难了,在19世纪初期才取得了最接近几颗恒星的值。即使在21世纪,恒星视差的测量已经达到银河系的尺度,但大多数的距离测量还是经由红移的计算或是其它的方法。
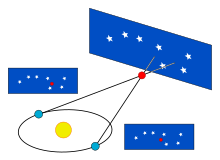
视差通常是由地球在轨道上不同的位置,导致观察到近距离的恒星相对于遥远的天体移动到不同位置获得的。经由观察视差,测量角度和利用三角学,可以测量不同物体在空间中的距离,通常是恒星,但在太空中的其它天体也可以。
因为其它的恒星都非常遥远,因此测量的角度都非常小,而且需要利用瘦三角形逼近,一个天体的距离 (以秒差距测量) 是视差值 (以角秒测量) 的倒数:
例如,比邻星的距离是1/0.7687=1.3009秒差距(4.243光年)[1]。 天鹅座61是第一颗成功测量出恒星视差的恒星,是贝塞耳在1838年于柯尼斯堡天文台使用夫琅和费的量日仪测出的[2][3]。
早期的理论和企图
编辑事实上,因为恒星视差非常小,因此一直未能观测到 (直到19世纪),并在近代史中被作为反对日心说的科学论据。很明显的,如果星星的距离够远,从欧几里得的几何学是无法察觉的,但由于种种的原因,使这种巨大的距离难以置信:其中之一是为了使缺乏视差的恒星能够相容,土星轨道和第八领域 (恒星) 之间必须有巨大而不太可能存在的空隙,使得第谷成为哥白尼日心说的主要反对者[4]。
詹姆斯·布拉德雷在1729年首度尝试测量恒星视差。他以望远镜证明恒星的运动是太微不足道的,但他发现了光行差[5]、地轴的章动、和编辑了3222颗恒星的星表。
19世纪和20世纪
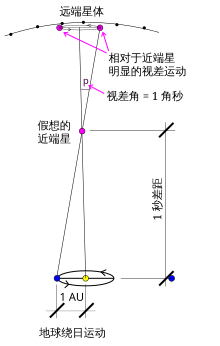
编辑恒星视差最常使用周年视差来测量,定义是从地球和太阳看见的恒星位置在角度上的差异,也就是一颗恒星在地球绕太阳轨道平均半径对角上的差别。1秒差距 (3.26光年) 的定义是周年视差为1角秒的距离。周年视差一般是观察在一年的不同时间里,通过地球在轨道上移动测量的恒星位置。周年视差的测量是第一个可靠的测量最接近的恒星距离的方法。第一次成功测量出的恒星视差是白塞耳在1838年使用量日仪测出的天鹅座61[2][6]。
由于测量上的困难,在19世纪结束时只有大约60颗的恒星视差被观察到,而且多数都是使用动丝测微器。在20世纪初期,使用天文照相底片的天文摄影仪加速了这个过程。自动的底片量测[7]和1960年代更精密的电脑技术使得星表的比对更有效率。 在1980年代,感光耦合元件 (CCD) 取代了照相底片,并且使不确定的因素减少到千分之一角秒。
恒星视差依然是校准其他测量方法的标准 (参见宇宙距离尺度)。基于恒星视差的距离计算需要很精确的测量地球到太阳的距离,现在是以雷达从行星表面的反射为基础[8]。
在这些计算中所涉及的角度都很小,因此很难衡量。最接近太阳的恒星 (因此这颗恒星有最大的视差),比邻星,的视差是0.7687 ± 0.0003角秒[1]。这相当于从5.3公里之外观察直径2厘米大小物体的弦所形成的角。
太空天文测量学的视差
编辑在1989年,依巴谷卫星发射的主要目的就是观察近距离恒星的视差和自行,这种方法使可测量数量增加了10倍。即便如此,依巴谷卫星能测量出视差角的恒星距离也只能达到1,600光年,相较于银河系的直径只比1%多了一点。欧洲太空总署的盖亚任务,于2000年推出,2013年3月发射升空,能够让视差角的测量精确度达到10微秒[9] 。在2018年释出的资料中[10], 能够绘制出邻近地球数万光年内恒星 (与潜在行星) 的位置图,将包括10亿颗恒星的位置、视差、和自行,所有的恒星在红色和蓝色的光度资料都可接受正规的标准误差。
其它基线
编辑太阳在空间中的运动提供了更长的基线,可以增加测量视差的准确性,称为长期视差。对于银河盘面中的恒星,这相当于每年平均4天文单位的基线,对银晕中的恒星是每年40天文单位。经过数十年,这个基线测量的视差数量极可以高于用传统的地球-太阳距离基线测量视差。不过,因为其它恒星的相对速度是一个未知的不确定值,长期视差也引入了较高的不确定性。当应用在多恒星的样本时可以减少不确定性,因为精确度反比于样本数量大小的平方根 [11]。
在天文学的其它视差
编辑相关条目
编辑参考资料
编辑- ^ 1.0 1.1 Benedict, G. Fritz; et al. Interferometric Astrometry of Proxima Centauri and Barnard's Star Using HUBBLE SPACE TELESCOPE Fine Guidance Sensor 3: Detection Limits for Substellar Companions. The Astronomical Journal. 1999, 118 (2): 1086–1100. Bibcode:1999astro.ph..5318B. doi:10.1086/300975.
- ^ 2.0 2.1 Zeilik & Gregory 1998,p. 44.
- ^ Alan W. Hirshfeld - Parallax: The Race to Measure the Cosmos (2002) - Page 259, Google Books 2010. [2012-02-15]. (原始内容存档于2015-04-16).
- ^ See p.51 in The reception of Copernicus' heliocentric theory: proceedings of a symposium organized by the Nicolas Copernicus Committee of the International Union of the History and Philosophy of Science, Torun, Poland, 1973, ed. Jerzy Dobrzycki, International Union of the History and Philosophy of Science. Nicolas Copernicus Committee; ISBN 9027703116, ISBN 9789027703118
- ^ Robert K. Buchheim - The sky is your laboratory: advanced astronomy projects for amateurs(2007) - Page 184, Google Books 2010
- ^ Bessel, FW, "Bestimmung der Entfernung des 61sten Sterns des Schwans 互联网档案馆的存档,存档日期2007-06-24." (1838) Astronomische Nachrichten, vol. 16, pp. 65-96.
- ^ CERN paper on plate measuring machine (页面存档备份,存于互联网档案馆) USNO StarScan
- ^ Zeilik & Gregory 1998,§ 22-3.
- ^ Henney, Paul J. ESA's Gaia Mission to study stars. Astronomy Today. [2008-03-08]. (原始内容存档于2008-03-17).
- ^ ESA, ESA. ESA's Gaia DR2. ESA. 2018 [2018-03-19]. (原始内容存档于2020-05-10).
- ^ Popowski, Piotr; Gould, Andrew. Mathematics of Statistical Parallax and the Local Distance Scale. 1998-01-29. arXiv:astro-ph/9703140
|class=被忽略 (帮助).
- Hirshfeld, Alan w. Parallax: The Race to Measure the Cosmos. New York: W. H. Freeman. 2001. ISBN 0716737116.
- Whipple, Fred L. Earth Moon and Planets. Read Books. 2007. ISBN 1406764132..
- Zeilik, Michael A.; Gregory, Stephan A. Introductory Astronomy & Astrophysics 4th. Saunders College Publishing. 1998. ISBN 0030062284..
延伸读物
编辑- Dyson, F. W. Measurement of the distances of the stars. The Observatory. 1915, 38: 292. Bibcode:1915Obs....38..292D.
