堆排序
堆排序(英语:Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构,并同时满足堆的性质:即子节点的键值或索引总是小于(或者大于)它的父节点。
| 堆排序 | |
|---|---|
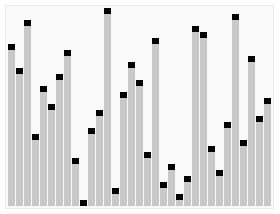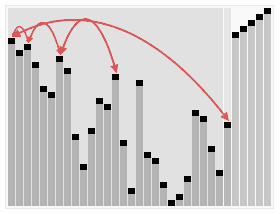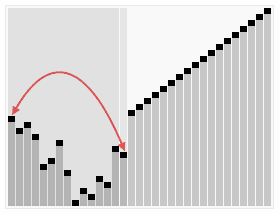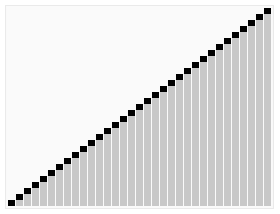 堆排序算法的演示。首先,将元素进行重排,以符合堆的条件。图中排序过程之前简单地绘出了堆树的结构。 | |
| 概况 | |
| 类别 | 排序算法 |
| 数据结构 | 数组 |
| 复杂度 | |
| 平均时间复杂度 | |
| 最坏时间复杂度 | |
| 最优时间复杂度 | [1] |
| 空间复杂度 | total, auxiliary |
| 最佳解 | 不是 |
| 相关变量的定义 | |
概述
编辑若以升序排序说明,把数组转换成最大堆(Max-Heap Heap),这是一种满足最大堆性质(Max-Heap Property)的二叉树:对于除了根之外的每个节点i, A[parent(i)] ≥ A[i]。
重复从最大堆取出数值最大的结点(把根结点和最后一个结点交换,把交换后的最后一个结点移出堆),并让残余的堆维持最大堆性质。
堆节点的访问
编辑通常堆是通过一维数组来实现的。在数组起始位置为0的情形中:
- 父节点i的左子节点在位置 ;
- 父节点i的右子节点在位置 ;
- 子节点i的父节点在位置 ;
堆的操作
编辑在堆的数据结构中,堆中的最大值总是位于根节点(在优先队列中使用堆的话堆中的最小值位于根节点)。堆中定义以下几种操作:
- 最大堆调整(Max Heapify):将堆的末端子节点作调整,使得子节点永远小于父节点
- 建立最大堆(Build Max Heap):将堆中的所有数据重新排序
- 堆排序(HeapSort):移除位在第一个数据的根节点,并做最大堆调整的递归运算
实现示例
编辑C语言
编辑#include <stdio.h>
#include <stdlib.h>
void swap(int *a, int *b) {
int temp = *b;
*b = *a;
*a = temp;
}
void max_heapify(int arr[], int start, int end) {
// 建立父節點指標和子節點指標
int dad = start;
int son = dad * 2 + 1;
while (son <= end) { // 若子節點指標在範圍內才做比較
if (son + 1 <= end && arr[son] < arr[son + 1]) // 先比較兩個子節點大小,選擇最大的
son++;
if (arr[dad] > arr[son]) //如果父節點大於子節點代表調整完畢,直接跳出函數
return;
else { // 否則交換父子內容再繼續子節點和孫節點比较
swap(&arr[dad], &arr[son]);
dad = son;
son = dad * 2 + 1;
}
}
}
void heap_sort(int arr[], int len) {
int i;
// 初始化,i從最後一個父節點開始調整
for (i = len / 2 - 1; i >= 0; i--)
max_heapify(arr, i, len - 1);
// 先將第一個元素和已排好元素前一位做交換,再重新調整,直到排序完畢
for (i = len - 1; i > 0; i--) {
swap(&arr[0], &arr[i]);
max_heapify(arr, 0, i - 1);
}
}
int main() {
int arr[] = { 3, 5, 3, 0, 8, 6, 1, 5, 8, 6, 2, 4, 9, 4, 7, 0, 1, 8, 9, 7, 3, 1, 2, 5, 9, 7, 4, 0, 2, 6 };
int len = (int) sizeof(arr) / sizeof(*arr);
heap_sort(arr, len);
int i;
for (i = 0; i < len; i++)
printf("%d ", arr[i]);
printf("\n");
return 0;
}
C++
编辑#include <iostream>
#include <algorithm>
using namespace std;
void max_heapify(int arr[], int start, int end) {
// 建立父節點指標和子節點指標
int dad = start;
int son = dad * 2 + 1;
while (son <= end) { // 若子節點指標在範圍內才做比較
if (son + 1 <= end && arr[son] < arr[son + 1]) // 先比較兩個子節點大小,選擇最大的
son++;
if (arr[dad] > arr[son]) // 如果父節點大於子節點代表調整完畢,直接跳出函數
return;
else { // 否則交換父子內容再繼續子節點和孫節點比較
swap(arr[dad], arr[son]);
dad = son;
son = dad * 2 + 1;
}
}
}
void heap_sort(int arr[], int len) {
// 初始化,i從最後一個父節點開始調整
for (int i = len / 2 - 1; i >= 0; i--)
max_heapify(arr, i, len - 1);
// 先將第一個元素和已经排好的元素前一位做交換,再從新調整(刚调整的元素之前的元素),直到排序完畢
for (int i = len - 1; i > 0; i--) {
swap(arr[0], arr[i]);
max_heapify(arr, 0, i - 1);
}
}
int main() {
int arr[] = { 3, 5, 3, 0, 8, 6, 1, 5, 8, 6, 2, 4, 9, 4, 7, 0, 1, 8, 9, 7, 3, 1, 2, 5, 9, 7, 4, 0, 2, 6 };
int len = (int) sizeof(arr) / sizeof(*arr);
heap_sort(arr, len);
for (int i = 0; i < len; i++)
cout << arr[i] << ' ';
cout << endl;
return 0;
}
Java
编辑import java.util.Arrays;
public class HeapSort {
private int[] arr;
public HeapSort(int[] arr) {
this.arr = arr;
}
/**
* 堆排序的主要入口方法,共两步。
*/
public void sort() {
/*
* 第一步:将数组堆化
* beginIndex = 第一个非叶子节点。
* 从第一个非叶子节点开始即可。无需从最后一个叶子节点开始。
* 叶子节点可以看作已符合堆要求的节点,根节点就是它自己且自己以下值为最大。
*/
int len = arr.length - 1;
int beginIndex = (arr.length >> 1)- 1;
for (int i = beginIndex; i >= 0; i--)
maxHeapify(i, len);
/*
* 第二步:对堆化数据排序
* 每次都是移出最顶层的根节点A[0],与最尾部节点位置调换,同时遍历长度 - 1。
* 然后从新整理被换到根节点的末尾元素,使其符合堆的特性。
* 直至未排序的堆长度为 0。
*/
for (int i = len; i > 0; i--) {
swap(0, i);
maxHeapify(0, i - 1);
}
}
private void swap(int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
/**
* 调整索引为 index 处的数据,使其符合堆的特性。
*
* @param index 需要堆化处理的数据的索引
* @param len 未排序的堆(数组)的长度
*/
private void maxHeapify(int index, int len) {
int li = (index << 1) + 1; // 左子节点索引
int ri = li + 1; // 右子节点索引
int cMax = li; // 子节点值最大索引,默认左子节点。
if (li > len) return; // 左子节点索引超出计算范围,直接返回。
if (ri <= len && arr[ri] > arr[li]) // 先判断左右子节点,哪个较大。
cMax = ri;
if (arr[cMax] > arr[index]) {
swap(cMax, index); // 如果父节点被子节点调换,
maxHeapify(cMax, len); // 则需要继续判断换下后的父节点是否符合堆的特性。
}
}
/**
* 测试用例
*
* 输出:
* [0, 0, 0, 1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4, 5, 5, 5, 6, 6, 6, 7, 7, 7, 8, 8, 8, 9, 9, 9]
*/
public static void main(String[] args) {
int[] arr = new int[] {3, 5, 3, 0, 8, 6, 1, 5, 8, 6, 2, 4, 9, 4, 7, 0, 1, 8, 9, 7, 3, 1, 2, 5, 9, 7, 4, 0, 2, 6};
new HeapSort(arr).sort();
System.out.println(Arrays.toString(arr));
}
}
Python
编辑#!/usr/bin/env python
#-*-coding:utf-8-*-
def heap_sort(lst):
def sift_down(start, end):
"""最大堆调整"""
root = start
while True:
child = 2 * root + 1
if child > end:
break
if child + 1 <= end and lst[child] < lst[child + 1]:
child += 1
if lst[root] < lst[child]:
lst[root], lst[child] = lst[child], lst[root]
root = child
else:
break
# 創建最大堆
for start in range((len(lst) - 2) // 2, -1, -1):
sift_down(start, len(lst) - 1)
# 堆排序
for end in range(len(lst) - 1, 0, -1):
lst[0], lst[end] = lst[end], lst[0]
sift_down(0, end - 1)
return lst
if __name__ == "__main__":
l = [9, 2, 1, 7, 6, 8, 5, 3, 4]
heap_sort(l)
JavaScript
编辑Array.prototype.heap_sort = function() {
var arr = this.slice(0);
function swap(i, j) {
var tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
function max_heapify(start, end) {
//建立父節點指標和子節點指標
var dad = start;
var son = dad * 2 + 1;
if (son >= end)//若子節點指標超過範圍直接跳出函數
return;
if (son + 1 < end && arr[son] < arr[son + 1])//先比較兩個子節點大小,選擇最大的
son++;
if (arr[dad] < arr[son]) {//如果父節點小於子節點時,交換父子內容再繼續子節點和孫節點比較
swap(dad, son);
max_heapify(son, end);
}
}
var len = arr.length;
//初始化,i從最後一個父節點開始調整
for (var i = Math.floor(len / 2) - 1; i >= 0; i--)
max_heapify(i, len);
//先將第一個元素和已排好元素前一位做交換,再從新調整,直到排序完畢
for (var i = len - 1; i > 0; i--) {
swap(0, i);
max_heapify(0, i);
}
return arr;
};
var a = [3, 5, 3, 0, 8, 6, 1, 5, 8, 6, 2, 4, 9, 4, 7, 0, 1, 8, 9, 7, 3, 1, 2, 5, 9, 7, 4, 0, 2, 6];
console.log(a.heap_sort());
PHP
编辑<?php
function swap(&$x, &$y) {
$t = $x;
$x = $y;
$y = $t;
}
function max_heapify(&$arr, $start, $end) {
//建立父節點指標和子節點指標
$dad = $start;
$son = $dad * 2 + 1;
if ($son >= $end)//若子節點指標超過範圍直接跳出函數
return;
if ($son + 1 < $end && $arr[$son] < $arr[$son + 1])//先比較兩個子節點大小,選擇最大的
$son++;
if ($arr[$dad] <= $arr[$son]) {//如果父節點小於子節點時,交換父子內容再繼續子節點和孫節點比較
swap($arr[$dad], $arr[$son]);
max_heapify($arr, $son, $end);
}
}
function heap_sort($arr) {
$len = count($arr);
//初始化,i從最後一個父節點開始調整
for ($i = ceil($len/2) - 1; $i >= 0; $i--)
max_heapify($arr, $i, $len);
//先將第一個元素和已排好元素前一位做交換,再從新調整,直到排序完畢
for ($i = $len - 1; $i > 0; $i--) {
swap($arr[0], $arr[$i]);
max_heapify($arr, 0, $i);
}
return $arr;
}
$arr = array(3, 5, 3, 0, 8, 6, 1, 5, 8, 6, 2, 4, 9, 4, 7, 0, 1, 8, 9, 7, 3, 1, 2, 5, 9, 7, 4, 0, 2, 6);
$arr = heap_sort($arr);
for ($i = 0; $i < count($arr); $i++)
echo $arr[$i] . ' ';
?>
Go
编辑package main
import (
"fmt"
)
func HeapSort(array []int) {
m := len(array)
s := m/2
for i := s; i > -1; i-- {
heap(array, i, m-1)
}
for i := m-1; i > 0; i-- {
array[i], array[0] = array[0], array[i]
heap(array, 0, i-1)
}
}
func heap(array []int, i, end int){
l := 2*i+1
if l > end {
return
}
n := l
r := 2*i+2
if r <= end && array[r]>array[l]{
n = r
}
if array[i] > array[n]{
return
}
array[n], array[i] = array[i], array[n]
heap(array, n, end)
}
func main() {
array := []int{
55, 94,87,1,4,32,11,77,39,42,64,53,70,12,9,
}
HeapSort(array)
fmt.Println(array)
}
function HeapSort(array)
function adjust(l,u)
while true
j = 2*l # 左子點
if (j>u) # 代表沒有子點
break
end
if ((j+1) <= u) # 有右子點
if (array[j] < array[j+1])
j += 1 #比較左右子點
end
end
if (array[j] > array[l]) #比較父點跟子點
array[l], array[j]= array[j], array[l]
l = j # 有交換
else
break # 沒交換跳出迴圈
end
end
end
n = length(array)
for i in n:-1:1 # 建 max Heap
adjust(i,n)
end
#持續把第一個(最大)的元素最後一個交換
array[n],array[1]=array[1],array[n]
for i in n-1:-1:1
adjust(1,i)
array[i],array[1]=array[1],array[i]
end
return array
end
Rust
编辑fn max_heapify<T: Ord + Copy>(data: &mut [T], pos: usize, end: usize) {
let mut dad = pos;
let mut son = dad * 2 + 1;
while son <= end {
if son < end && data[son] < data[son + 1] {
son += 1;
}
if data[dad] > data[son] {
return;
} else {
data.swap(dad, son);
dad = son;
son = dad * 2 + 1;
}
}
}
fn heap_sort<T:Ord+Copy>(data: &mut[T]) {
let len = data.len();
for i in (0..=len / 2 - 1).rev() {
max_heapify(data, i, len - 1);
}
for i in (1..=len - 1).rev() {
data.swap(0, i);
max_heapify(data, 0, i - 1);
}
}
fn main() {
let mut nums = vec![9, 2, 1, 7, 6, 8, 5, 3, 4];
heap_sort(nums.as_mut_slice());
}
原地堆排序
编辑基于以上堆相关的操作,我们可以很容易的定义堆排序。例如,假设我们已经读入一系列数据并创建了一个堆,一个最直观的算法就是反复的调用del_max()函数,因为该函数总是能够返回堆中最大的值,然后把它从堆中删除,从而对这一系列返回值的输出就得到了该序列的降序排列。真正的原地堆排序使用了另外一个小技巧。堆排序的过程是:
- 建立一个堆
- 把堆首(最大值)和堆尾互换
- 把堆的尺寸缩小1,并调用
shift_down(0),目的是把新的数组顶端数据调整到相应位置 - 重复步骤2,直到堆的尺寸为1
平均复杂度
编辑参考
编辑- ^ R. Schaffer, R. Sedgewick. The Analysis of Heapsort. Journal of Algorithms. 1993-07, 15 (1): 76–100 [2022-10-02]. doi:10.1006/jagm.1993.1031. (原始内容存档于2022-01-27) (英语).
外部链接
编辑- 常见排序算法 - 堆排序 (Heap Sort)
- 堆算法的可视化演示 可以直观看到堆算法的操作




