(證明的思路是用數學歸納法 證明正整數的情形,並推廣到負整數。)
令
P
(
n
)
=
(
cos
θ
+
i
sin
θ
)
n
=
cos
(
n
θ
)
+
i
sin
(
n
θ
)
,
n
∈
N
{\displaystyle P(n)=(\cos \theta +i\sin \theta )^{n}=\cos(n\theta )+i\sin(n\theta ),n\in \mathbb {N} }
(1)當
n
=
0
{\displaystyle n=0}
(2)當
n
=
1
{\displaystyle n=1}
左式
=
(
cos
θ
+
i
sin
θ
)
1
=
cos
θ
+
i
sin
θ
=
cos
(
1
⋅
θ
)
+
i
sin
(
1
⋅
θ
)
=
{\displaystyle =(\cos \theta +i\sin \theta )^{1}=\cos \theta +i\sin \theta =\cos(1\cdot \theta )+i\sin(1\cdot \theta )=}
因此,
P
(
1
)
{\displaystyle P(1)}
(3)當
n
>
1
{\displaystyle n>1}
假設
P
(
k
)
{\displaystyle P(k)}
(
cos
θ
+
i
sin
θ
)
k
=
cos
(
k
θ
)
+
i
sin
(
k
θ
)
{\displaystyle (\cos \theta +i\sin \theta )^{k}=\cos(k\theta )+i\sin(k\theta )}
當
n
=
k
+
1
{\displaystyle n=k+1}
(
cos
θ
+
i
sin
θ
)
k
+
1
=
(
cos
θ
+
i
sin
θ
)
k
⋅
(
cos
θ
+
i
sin
θ
)
=
(
cos
k
θ
+
i
sin
k
θ
)
⋅
(
cos
θ
+
i
sin
θ
)
=
(
cos
k
θ
⋅
cos
θ
+
i
sin
k
θ
⋅
i
sin
θ
)
+
(
cos
k
θ
⋅
i
sin
θ
+
i
sin
k
θ
⋅
cos
θ
)
=
(
cos
k
θ
⋅
cos
θ
−
sin
k
θ
⋅
sin
θ
)
+
i
(
cos
k
θ
⋅
sin
θ
+
sin
k
θ
⋅
cos
θ
)
=
1
cos
(
k
θ
+
θ
)
+
i
sin
(
k
θ
+
θ
)
=
cos
[
(
k
+
1
)
θ
]
+
i
sin
[
(
k
+
1
)
θ
]
{\displaystyle {\begin{aligned}(\cos \theta +i\sin \theta )^{k+1}&=(\cos \theta +i\sin \theta )^{k}\cdot (\cos \theta +i\sin \theta )\\&=(\cos k\theta +i\sin k\theta )\cdot (\cos \theta +i\sin \theta )\\&=(\cos k\theta \cdot \cos \theta +i\sin k\theta \cdot i\sin \theta )+(\cos k\theta \cdot i\sin \theta +i\sin k\theta \cdot \cos \theta )\\&=(\cos k\theta \cdot \cos \theta -\sin k\theta \cdot \sin \theta )+i(\cos k\theta \cdot \sin \theta +\sin k\theta \cdot \cos \theta )\\&\ {\overset {1}{=}}\cos(k\theta +\theta )+i\sin(k\theta +\theta )\\&\ =\cos[(k+1)\theta ]+i\sin[(k+1)\theta ]\\\end{aligned}}}
等號1處使用和角公式 。
因此,
P
(
k
+
1
)
{\displaystyle P(k+1)}
綜上所述,根據數學歸納法,
∀
n
∈
N
{\displaystyle \forall n\in \mathbb {N} }
P
(
n
)
{\displaystyle P(n)}
另外,由恆等式:
(
cos
(
n
θ
)
+
i
sin
(
n
θ
)
)
⋅
(
cos
(
−
n
θ
)
+
i
sin
(
−
n
θ
)
)
=
1
{\displaystyle (\cos(n\theta )+i\sin(n\theta ))\cdot (\cos(-n\theta )+i\sin(-n\theta ))=1}
可知,公式對於負整數情況也成立。
證畢。
最簡單的方法是應用歐拉公式 [ 2]
由於
e
i
x
=
cos
x
+
i
sin
x
{\displaystyle e^{ix}=\cos x+i\sin x\,}
所以
(
cos
x
+
i
sin
x
)
n
=
(
e
i
x
)
n
=
e
i
n
x
=
e
i
(
n
x
)
=
cos
(
n
x
)
+
i
sin
(
n
x
)
{\displaystyle {\color {Green}(\cos x+i\sin x)^{n}}=(e^{ix})^{n}=e^{inx}=e^{i(nx)}={\color {Green}\cos(nx)+i\sin(nx)}}
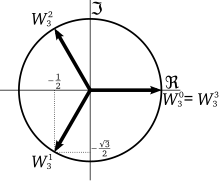
此定理可用來求單位複數的
n
{\displaystyle n}
|
z
|
=
1
{\displaystyle |z|=1}
z
=
cos
θ
+
i
sin
θ
{\displaystyle z=\cos \theta +i\sin \theta }
若
w
n
=
z
{\displaystyle w^{n}=z}
w
{\displaystyle w}
w
=
cos
ϕ
+
i
sin
ϕ
{\displaystyle w=\cos \phi +i\sin \phi }
按照狄默夫公式:
w
n
=
(
cos
ϕ
+
i
sin
ϕ
)
n
=
cos
n
ϕ
+
i
sin
n
ϕ
=
cos
θ
+
i
sin
θ
=
z
{\displaystyle w^{n}=(\cos \phi +i\sin \phi )^{n}=\cos n\phi +i\sin n\phi =\cos \theta +i\sin \theta =z}
於是得到
n
ϕ
=
θ
+
2
k
π
{\displaystyle n\phi =\theta +2k\pi }
k
∈
Z
{\displaystyle k\in \mathbb {Z} }
也就是:
ϕ
=
θ
+
2
k
π
n
{\displaystyle \phi ={\dfrac {\theta +2k\pi }{n}}}
當
k
{\displaystyle k}
0
,
1
,
…
,
n
−
1
{\displaystyle 0,1,\ldots ,n-1}
n
{\displaystyle n}
w
=
cos
(
θ
+
2
k
π
n
)
+
i
sin
(
θ
+
2
k
π
n
)
,
k
=
0
,
1
,
…
,
n
−
1
{\displaystyle w=\cos({\dfrac {\theta +2k\pi }{n}})+i\sin({\dfrac {\theta +2k\pi }{n}}),k=0,1,\ldots ,n-1}
^ Lial, Margaret L.; Hornsby, John; Schneider, David I.; Callie J., Daniels. College Algebra and Trigonometry 4th. Boston: Pearson/Addison Wesley. 2008: 792. ISBN 9780321497444 ^ 林琦焜. 棣美弗定理與 Euler 公式 (PDF) . 中央研究院 . 2006-12-22 [2017-06-18 ] . (原始內容存檔 (PDF) 於2021-01-19).