萨吕法则
萨吕法则(Sarrus' rule)是计算3×3矩阵行列式的记忆术,得名自19世纪的法国数学家皮埃尔·弗雷德里克·萨吕[1]。

考虑3×3矩阵
其行列式可以用以下方式计算:
将前二直行的数值写在第三行的右边,让矩阵变成一个五行的列矩阵,然后将从左上到右下对角线(图中的实线部份)数字的乘积和减去将从右上到左下对角线(图中的虚线部份)数字的乘积和,可以得到[1][2]:
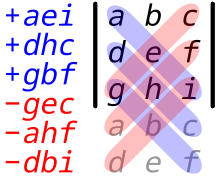
类似方式也可以计算2×2矩阵的行列式[1]:
萨吕法则是莱布尼茨行列式公式的特例,不适用于4×4或是更大的矩阵。萨吕法则也可以用3×3矩阵的拉普拉斯展开求得[1]。
另一种记忆萨吕法则的方式是想像矩阵是写在圆柱表面,让矩阵的左边和右边是连通的。
参考资料
编辑- Khattar, Dinesh. The Pearson Guide to Complete Mathematics for AIEEE 3rd. Pearson Education India. 2010: 6-2 [2016-04-01]. ISBN 978-81-317-2126-1. (原始内容存档于2014-10-22).
外部链接
编辑- Sarrus' rule at Planetmath (页面存档备份,存于互联网档案馆)
- Linear Algebra: Rule of Sarrus of Determinants (页面存档备份,存于互联网档案馆) at khanacademy.org


