扭棱
在几何学中,扭棱是一种多面体变换。该术语起源于开普勒对阿基米德立体的命名,分别为扭棱立方体(英语:snub cube、拉丁语:cubus simus)和扭棱十二面体(英语:snub dodecahedron、拉丁语:dodecaedron simum)[1][2]。一般而言,多面体经扭棱变换后可以形成两种互为手性镜像的形式,分别为顺时针方向的扭棱和逆时针方向的扭棱。以开普勒的命名对应的扭棱变换可以看做是正多面体的扩张,也就是将正多面体的面向外分开,并围绕著中心扭曲(不改变面的形状),然后加入以每个原始立体顶点为中心的正方形,并在每个原始立体之边的位置上加入成对的三角形来构成。[3]:99

 扭棱立方体或 扭棱截半立方体 |
 扭棱十二面体或 扭棱截半十二面体 |
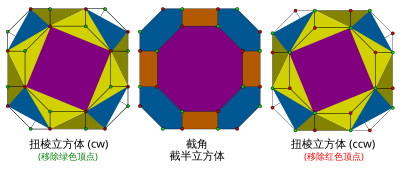

考克斯特对扭棱进行了推广,推广成能用于更广泛的均匀多面体,其定义略有不同。
康威扭棱
编辑康威研究了广义的多面体变换,定义了现在称为康威多面体表示法的多面体变换表示法,其可以运用在多面体和各种镶嵌或密铺的几何形状。康威称考克斯特定义的扭棱变换为半扭棱变换。[5]
在康威多面体表示法中,扭棱变换(康威表示法:s)被定义为陀螺变换(英语:gyro,康威表示法:g,为每个n边形面被切割成n个五边形的多面体变换)的对偶多面体(康威表示法:d),即康威表示法s = dg = dgd[6],其等价于先经截半变换再做截角变换后进行交替截角。康威表示法本身避免了考克斯特的交错(半)变换,因为它仅适用于仅具有偶数边数的面之多面体。
| 扭棱的形式 | 多面体 | 平面镶嵌 | 双曲镶嵌 | |||
|---|---|---|---|---|---|---|
| 原像名称 | 正四面体 | 立方体或 正八面体 |
正二十面体或 正十二面体 |
正方形镶嵌 | 正六边形镶嵌或 正三角形镶嵌 |
正七边形镶嵌或 七阶三角形镶嵌 |
| 图像 | ||||||
| 扭棱结果的康威表示法 | sT | sC = sO | sI = sD | sQ | sH = sΔ | sΔ7 |
| 图像 | 扭棱四面体 (正二十面体) |
扭棱立方体 |
扭棱十二面体 |
扭棱正方形镶嵌 |
扭棱六边形镶嵌 |
扭棱七边形镶嵌 |
在四维空间中,康威建议将扭棱二十四胞体称为半扭棱二十四胞体。与三维的扭棱多面体不同,三维的扭棱多面体是交替的全截(omnitruncation,即先截半再截角)的形式,而扭棱二十四胞体并非是正二十四胞体交替的全截的形式。事实上,扭棱二十四胞体是交替截角的正二十四胞体[7]。
考克斯特扭棱
编辑| 原像 | 截半 r |
截角 t |
交错 h | |
|---|---|---|---|---|
| 名称 | 立方体 | 截半立方体 | 截角截半立方体 全截立方体 |
扭棱截半立方体 |
| 康威表示法 | C | CO rC |
tCO trC或trO |
htCO = sCO htrC = srC |
| 施莱夫利符号 | {4,3} | 或r{4,3} | 或tr{4,3} | htr{4,3} = sr{4,3} |
| 考克斯特图 | 或 | 或 | 或 | |
| 图像 |
考克斯特扭棱的定义略有不同,其将扭棱定义为截角后交错,在这个定义下,扭棱立方体被视为扭棱后的截半立方体、扭棱十二面体被视为扭棱后的截半十二面体。在这种定义下命名的詹森多面体有扭棱锲形体和扭棱四角反角柱。这种命名在高维多胞体中也有所使用,如扩展施莱夫利符号记为s{3,4,3},并在考克斯特—迪肯符号记为 的扭棱二十四胞体[8]。
一个正多面体或镶嵌若在施莱夫利符号记为 且考克斯特—迪肯符号记为 ,则其截角后的像施莱夫利符号记为 、考克斯特—迪肯符号记为 ,若再将这个结果进行交错变换,则其变换后的像施莱夫利符号记为 、考克斯特—迪肯符号记为 。要完成这个交错变换,q必须为偶数[9]。
一个拟正多面体若在施莱夫利符号记为 或r{p,q}、考克斯特—迪肯符号记为 或 ,则其截角的像施莱夫利符号记为 或tr{p,q},则这个拟正多面体的扭棱可以定义为交错的截角截半立体 或 htr{p,q} = sr{p,q},和 or 。
例如,以开普勒的扭棱立方体是扭棱自拟正的截半立方体,而截半立方体的竖式施莱夫利符号记为 [10]、考克斯特—迪肯符号记为 ,所以扭棱立方体的竖式施莱夫利符号记为 [11]、考克斯特—迪肯符号记为 。扭棱立方体亦可以视为经过交错变换的截角截半立方体,截角截半立方体的竖式施莱夫利符号记为 [12]、考克斯特—迪肯符号记为 。[13]
顶点分支度为偶数的正多面体也可以进行截角后交错的扭棱,例如扭棱八面体,施莱夫利符号 、考克斯特—迪肯符号 ,其为交错的截角八面体施莱夫利符号 [14]、考克斯特—迪肯符号 。八面体在这种定义下的扭棱结果称为伪二十面体,一个拓朴与正二十面体完全相同但具备五角十二面体群对称性的立体[15]。
| 原像 | 截角 t |
交错 h | |
|---|---|---|---|
| 名称 | 正八面体 | 截角八面体 | 扭棱八面体 |
| 康威表示法 | O | tO | htO or sO |
| 施莱夫利符号 | {3,4} | t{3,4} | ht{3,4} = s{3,4} |
| 考克斯特符号 | |||
| 图像 |
考克斯特扭棱也允许将反棱柱的施莱夫利符号定义为 [16]:403或 ,基于n角柱的 或 。其中 是一个退化的n面形,其可以视为由二角形镶嵌球面的几何结构。
| 图像 | ||||||||
|---|---|---|---|---|---|---|---|---|
| 考克斯特 符号 |
|
|
|
|
|
|
... ... |
|
| 施莱夫利 符号 |
s{2,4} | s{2,6} | s{2,8} | s{2,10} | s{2,12} | s{2,14} | s{2,16}... | s{2,∞} |
| sr{2,2} |
sr{2,3} |
sr{2,4} |
sr{2,5} |
sr{2,6} |
sr{2,7} |
sr{2,8}... ... |
sr{2,∞} | |
| 康威 表示法 |
A2 = T | A3 = O | A4 | A5 | A6 | A7 | A8... | A∞ |
非均匀多面体的扭棱
编辑非均匀多面体也可以扭棱,但需要满足考克斯特扭棱的条件。考克斯特扭棱只能作用在顶点分支度全为偶数的立体上[13]。这允许了许多多面体的扭棱,包括了无穷集合的立体。例如:
| 扭棱双四角锥 |
|---|
| 扭棱双六角锥 |
| 图像 | ... | |||
|---|---|---|---|---|
| 名称 | 扭棱二角 反角柱 |
扭棱三角 反角柱 |
扭棱四角 反角柱 |
扭棱五角 反角柱 |
| 施莱夫利 符号 |
ss{2,4} | ss{2,6} | ss{2,8} | ss{2,10}... |
| ssr{2,2} |
ssr{2,3} |
ssr{2,4} |
ssr{2,5}... |
考克斯特的均匀扭棱星形多面体
编辑扭棱均匀星形多面体由其施瓦茨三角形(p q r)构造,具有合理有序的镜像对称角,且所有镜像都处于活动和交替的状态[17]。
| s{3/2,3/2} |
s{(3,3,5/2)} |
sr{5,5/2} |
s{(3,5,5/3)} |
sr{5/2,3} |
| sr{5/3,5} |
s{(5/2,5/3,3)} |
sr{5/3,3} |
s{(3/2,3/2,5/2)} |
s{3/2,5/3} |
参见
编辑| 原像 | 截角 | 截半 | 过截角 | 对偶 | 扩展 | 全截 | 交错 | ||
|---|---|---|---|---|---|---|---|---|---|
| 半变换 | 扭棱 | ||||||||
| t0{p,q} {p,q} |
t01{p,q} t{p,q} |
t1{p,q} r{p,q} |
t12{p,q} 2t{p,q} |
t2{p,q} 2r{p,q} |
t02{p,q} rr{p,q} |
t012{p,q} tr{p,q} |
ht0{p,q} h{q,p} |
ht12{p,q} s{q,p} |
ht012{p,q} sr{p,q} |
参考文献
编辑- ^ Kepler. Harmonices Mundi. 1619.
- ^ Coxeter. Chapter 3: Wythoff's Construction for Uniform Polytopes. The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 978-0-486-40919-1.
- ^ Holme, Audun. Geometry: Our Cultural Heritage. Springer Science & Business Media. 2010-09-23. ISBN 978-3-642-14441-7 (英语).
- ^ 4.0 4.1 John H. Conway; Heidi Burgiel; Chaim Goodman-Strass. The Symmetries of Things. 2008. ISBN 978-1-56881-220-5.
- ^ Conway, (2008)[4] Coxeter's semi-snub operation
- ^ polyHédronisme. levskaya.github.io. [2022-10-15]. (原始内容存档于2013-06-07).
- ^ Conway, (2008)[4] p.401 Gosset's Semi-snub Polyoctahedron
- ^ Klitzing, Richard. Snubs, Alternated Facetings, & Stott-coxeter-dynkin Diagrams. Symmetry-Culture and Science (Symmetrion 29 etvs st, budapest, 1067, hungary). 2010, 21 (4): 329–344.
- ^ Heckman, Gert, coxeter groups (PDF), 2018 [2022-08-25], (原始内容存档 (PDF)于2022-02-21)
- ^ Weisstein, Eric W. (编). Cuboctahedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Weisstein, Eric W. (编). Snub Cube. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Weisstein, Eric W. (编). Great Rhombicuboctahedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ 13.0 13.1 Coxeter, H. S. M. Regular and semi-regular polytopes. II. Mathematische Zeitschrift. 1985-12, 188 (4). ISSN 0025-5874. doi:10.1007/BF01161657 (英语).
- ^ Weisstein, Eric W. (编). Truncated Octahedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ John Baez. Fool's Gold. 2011-09-11 [2022-08-25]. (原始内容存档于2018-05-19).
- ^ Coxeter, Harold Scott MacDonald; Longuet-Higgins, M. S.; Miller, J. C. P. Uniform polyhedra. Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences (The Royal Society). 1954, 246 (916): 401–450 [2022-10-15]. Bibcode:1954RSPTA.246..401C. ISSN 0080-4614. JSTOR 91532. MR 0062446. S2CID 202575183. doi:10.1098/rsta.1954.0003. (原始内容存档于2020-09-18).
- ^ Maeder, Roman. The Wythoff Symbol. MathConsult. [2022-08-25]. (原始内容存档于2022-07-03).
- Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8 (pp. 154–156 8.6 Partial truncation, or alternation)
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1] (页面存档备份,存于互联网档案馆), Googlebooks [2]
- (Paper 17) Coxeter, The Evolution of Coxeter–Dynkin diagrams, [Nieuw Archief voor Wiskunde 9 (1991) 233–248]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380–407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559–591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3–45]
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5
- 埃里克·韦斯坦因. Snubification. MathWorld.