截角 (几何)
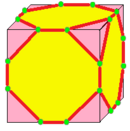 截角示意图,其将欲截去顶点的位置标记出来。 | ||
|---|---|---|
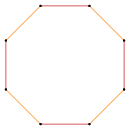 截角的正方形是一个 正八边形[1]: t{4} = {8} |
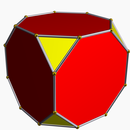 截角的立方体是一个 截角立方体[2]: t{4,3} 或 |
 截角的立方体堆砌是一个 截角立方体堆砌[3]: t{4,3,4} 或 |
在几何学中,截角[4]是一种将几何形状之顶点截去的操作,也就是一种将多边形、多面体、密铺、镶嵌或更高维的多胞体切去顶点,并在切去的顶点建立新的面、边与顶点的一种多面体变换[5]。这个词来自开普勒为阿基米德立体命的名称,其中有七种阿基米德立体可使用柏拉图立体套用截角变换构造[6]。
定义
编辑在几何学中,截角是一种针对多面体或多胞形的变换,若有一个多胞形P,则对P的截角计为tP,其定义为对P截角会产生一个新的多胞形tP,该多胞形为截去P的所有顶点,并将被截去的部分以该顶点对应的顶点图替换之,而此项由顶点图替换的元素称为截面。一个多胞形P的截角结果tP一般会由两种维面组成,一是截角变换产生的截面、二是多胞形P原本的维面被截角后的像。未截去所有顶点的截角操作称为部分截角(partial truncate)[7],如部分截角截四阶角五角二十四面体(只截特定角的五角二十四面体)、截对角六方偏方面体(截顶角的偏方面体)或平截头体(截顶角的锥体,又称锥台)[8]。由于有时某些立体的部分截角通常以截角称呼,因此部分文献会用完全截角(Fully truncate)来区分这种情况[9]。
均匀截角
编辑一般而言,任何多面体都可以以任何深度或角度进行截角,但也有一些切法符合所谓正规或均匀多面体的标准,例如:康威多面体表示法中的t(截角操作)[10]。
若不是任意截角的话,就是特殊的截角。特殊的截角通常暗示著它是一个均匀的截角,也就是说,施加在正多面体上会得到一个等边的半正多面体或均匀多面体。它的几何意义是固定的,就像正多面体[11]。
截角多边形
编辑一个若多边形的边数为n,则截角后会形成边数为2n的多边形,换句话说n边形的截角结果为2n边形。举例来说,三角形的截角结果通常为六边形[12]。而多边形的最大截角,即截角截至中点(又称截半)则会导致多边形变为对偶多边形[13]。
| {3} |
t{3} = {6} |
r{3} = {3} |
截角多面体或更高维的图形
编辑当截角一词被用在正多面体或正镶嵌图上时,通常代表“均匀截角”[14],其通常代表截角截至所有面都是正多边形的深度。
上表则展示了立方体透过截角深度不断加深的截角变换将立方体变换为截角立方体和截半立方体的过程。
若原像在施莱夫利符号中计为{p,q,...},则在上图表中间的紫色截角结果可以记为t{p,q,...}[15]。而截半为截角截到原本的棱消失,因此截半也称为完全截角[16]。
继续更深入地截角同样可以产生被截之面为正多边形面的均匀截角形式。比截半再更深入的均匀截角形式为过截角。过截角的效果为移除多面体面的所有边,但有保留部分多面体原有面的内部之局部。截角八面体则为立方体套用过截角变换后的像。[17]
过截角同样也存在完全截角的形式,即完全过截角,又称为过截半或双截半。其效果为截角截到原有面消失的深度[18]。大部分的三维图形经过过截半变换后会转变为对偶多面体,例如正八面体为立方体过截半的结果,在施莱夫利符号中可以用2r{4,3}表示。
| 原像 | 较浅的截角 | 均匀截角 | 较深的截角 | 截半 | 过截角 | 对偶 |
|---|---|---|---|---|---|---|
| 正四面体 |
截角四面体 |
正八面体 |
截角四面体 |
正四面体 | ||
| 正八面体 |
截角八面体 |
截半立方体 |
截角立方体 |
立方体 | ||
| 正二十面体 |
截角二十面体 |
截半二十面体 |
截角十二面体 |
正十二面体 | ||
| 小星形十二面体 |
截角小星形十二面体 |
截半大十二面体 |
截角大十二面体 |
大十二面体 | ||
| 大星形十二面体 |
截角大星形十二面体 |
大截半二十面体 |
截角大二十面体 |
大二十面体 |
裁边
编辑裁边又称截边、裁棱或截棱是一种与截角类似的操作,其为将一个几何结构的所有棱或边切去。裁边在三维空间中称为倒角,其结果为将多面体的所有棱替换成六边形面[19]。在四维空间中则会使几何结构的所有棱被替换为双角锥柱形状的胞[20]。
广义截角
编辑线性的截角可以推广到负的截角深度,或截到中点后将边反向连接形成边自相交的多边形作为截角深度更深的截角结果,这种截角有时称为超截角或星形截角。透过这种广义的截角可以行称一些星形多面体和一些均匀多面体。[21]
- 浅截角:原有边的长度减短、面被截成边数为原有边数两倍的多边形,且截面以旧顶点为中心。[22]
- 反截角:一种与浅截角相反的截角[23]。
- 均匀截角:截角结果为所有棱等长的各类截角之特例[14][15]。
- 完全截角:又称截半,为浅截角的极限,其结果会使原有几何图形的边变成一个点[16]。
- 超截角:比截半更深入的截角形式,由于超出了截半的截角深度,其使原始的边反转(向外延伸到截面),并导致出现同一立体面与边自我相交的情况。[24]
- 星形截角:比超截角更深入的截角。若将一般的截角视为将面向外移动并将空处补上截面(例如截角的正方形为八边形,可以视为将正方形的四条边远离几何中心再将4个空隙处补上截边),则星形截角则可以视为面的处理与一般截角反向的截角结果(例如星形截角的正方形为八边形,可以视为将正方形的四条边向几何中心靠近,此时四条边两两相交,再将4个空隙处补上截边,形成星形八边形),其可以将部分几何图形转变成星形[25]。
| ⇨ |
立方体 {4,3} |
⇨ |
截角 t{4,3} |
⇨ |
截半 r{4,3} |
⇩ |
| 反截角 |
超截角 | |||||
| ⇧ |
星形截半 |
⇦ |
星形截角 t{4/3,3} |
⇦ |
超截半 |
⇦ |
参见
编辑参考文献
编辑- ^ Wenninger, Magnus J. Polyhedron Models. Cambridge University Press. 1974-04-26: 9. ISBN 978-0-521-09859-5 (英语).
- ^ Weisstein, Eric W. (编). Truncated Cube. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ George Olshevsky, Uniform Panoploid Tetracombs, Manuscript (2006) (包含11个凸半正镶嵌、28个凸半正堆砌、和143个凸半正四维砌的全表)
- ^ 截尖,截角 - 學術名詞:工程圖學. 双语词汇、学术名词暨辞书资讯网. 国家教育研究院. [2017-02-21]. (原始内容存档于2017-02-22).
- ^ Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8 (pp. 145–154 Chapter 8: Truncation)
- ^ Weisstein, Eric W. (编). Truncation. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Olshevsky, George, Truncation at Glossary for Hyperspace.
- ^ William F. Kern, James R. Bland, Solid Mensuration with proofs, 1938, p. 67
- ^ Berman, Leah Wrenn; Monson, Barry; Oliveros, Déborah; Williams, Gordon I. Fully truncated simplices and their monodromy groups. Advances in Geometry. 2018-04-25, 18 (2) [2022-10-15]. ISSN 1615-7168. doi:10.1515/advgeom-2017-0047. (原始内容存档于2022-10-16) (英语).
- ^ George W. Hart. Conway Notation for Polyhedra. Virtual Polyhedra. 1998 [2019-11-05]. (原始内容存档于2014-11-29).
- ^ Norman Johnson Uniform Polytopes, Manuscript (1991)
- ^ The Truncations. science.larouchepac.com. [2019-10-16]. (原始内容存档于2016-01-17).
- ^ Reid, Samuel. Rectifications of Convex Polyhedra. arXiv preprint arXiv:1604.00580. 2016. arXiv:1604.00580 . doi:10.48550/arXiv.1604.00580.
- ^ 14.0 14.1 N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- ^ 15.0 15.1 Kaleidoscopes: Selected Writings of H.S.M. Coxeter | Wiley. Wiley.com. [2022-10-15]. (原始内容存档于2022-05-25) (美国英语).
- ^ 16.0 16.1 Grabowiecka, Zofia. The decoration of a Coxeter—Dynkin diagram and the Schläfli symbol as two methods to describe polytopes generated by finite reflection groups. Journal of Physics: Conference Series. 2019-04, 1194 [2022-10-15]. ISSN 1742-6588. doi:10.1088/1742-6596/1194/1/012039. (原始内容存档于2022-10-19).
- ^ Diudea, M.V. Multi-shell Polyhedral Clusters. Carbon Materials: Chemistry and Physics. Springer International Publishing. 2017: 26. ISBN 9783319641232.
- ^ Tony Forbes. Regular polytopes (PDF). maths.qmul.ac.uk. December 2014 [2019-10-17]. (原始内容 (PDF)存档于2018-10-08).
- ^ Dr. Richard Klitzing. cube-trunc-rad, Polytopes & their Incidence Matrices. bendwavy.org. [2019-11-05]. (原始内容存档于2019-11-05).
- ^ Richmond S. Newman. Crystallization in systems of hard polyhedra (PDF). semanticscholar.org. [2019-11-05]. (原始内容 (PDF)存档于2019-11-05).
- ^ Ragnar Torfason. Polyhedron Models for the Classroom. theweebsite.com. 2006-06-03 [2019-10-22]. (原始内容存档于2013-06-10).
- ^ Yackel, C. and belcastro, sarah-marie. Figuring Fibers. Miscellaneous Books. American Mathematical Society. 2018: 146 [2019-10-22]. ISBN 9781470429317. LCCN 2018033586. (原始内容存档于2019-11-29).
- ^ truncation. 2015-07-01 [2019-10-22]. (原始内容存档于2019-04-14).
- ^ Truncated Polytopes. bendwavy.org. [2019-10-28]. (原始内容存档于2019-05-13).
- ^ Stellated Truncated Hexahedron. software3d.com. [2019-10-28]. (原始内容存档于2019-10-28).
外部链接
编辑- 埃里克·韦斯坦因. Truncation. MathWorld.
- Olshevsky, George, Truncation at Glossary for Hyperspace.
- Polyhedra Names, truncation (页面存档备份,存于互联网档案馆)
| 原像 | 截角 | 截半 | 过截角 | 对偶 | 扩展 | 全截 | 交错 | ||
|---|---|---|---|---|---|---|---|---|---|
| 半变换 | 扭棱 | ||||||||
| t0{p,q} {p,q} |
t01{p,q} t{p,q} |
t1{p,q} r{p,q} |
t12{p,q} 2t{p,q} |
t2{p,q} 2r{p,q} |
t02{p,q} rr{p,q} |
t012{p,q} tr{p,q} |
ht0{p,q} h{q,p} |
ht12{p,q} s{q,p} |
ht012{p,q} sr{p,q} |