小双三角十二面截半二十面体

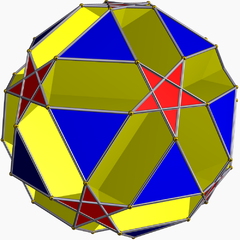
小双三角十二面截半二十面体又称小十二面化截半二十面体（small dodekified icosidodecahedron）是一种星形均匀多面体，由20个正三角形、12个正五角星和12个正十边形组成，索引为U₄₃，对偶多面体为小双三角十二角星化六十面体，具有二十面体群对称性。。

小双三角十二面截半二十面体

类别	均匀星形多面体
对偶多面体	小双三角十二角星化六十面体
识别
名称	小双三角十二面截半二十面体 Small ditrigonal dodecicosidodecahedron small dodekified icosidodecahedron
参考索引	U43, C55, W82
鲍尔斯缩写	sidditdid
数学表示法
威佐夫符号	5/3 3 | 5 5/2 3/2 | 5
性质
面	44
边	120
顶点	60
欧拉特征数	F=44, E=120, V=60 （χ=-16）
组成与布局
面的种类	20个正三角形 12个正五角星 12个正十边形
顶点图	3.10.5/3.10
对称性
对称群	Ih, [5,3], *532
图像
3.10.5/3.10 （顶点图） 小双三角十二角星化六十面体 （对偶多面体）

性质

小双三角十二面截半二十面体共由44个面、120条边和60个顶点组成。在其44个面中，有20个正三角形面、12个正五角星面和12个正十边形面，或以施莱夫利符号表示为20{3}+12{5⁄2}+12{10}。在其60个顶点中，每个顶点都是2个十边形面、1个三角形面和1个五角星面的公共顶点，并且这些面在构成顶角的多面角时，以五角星、十边形、三角形和十边形的顺序排列，在顶点图中可以用(5/3.10.3.10)或(10.5/3.10.3)来表示。

表示法

小双三角十二面截半二十面体在考克斯特—迪肯符号中可以表示为（x5/3o3x5*a）或（x3/2o5/2x5*a），在威佐夫记号中可以表示为5/3 3 | 5。

尺寸

若小双三角十二面截半二十面体的边长为单位长，则其外接球半径为：

$R={\frac {34+6{\sqrt {5}}}{4}}\approx 1.72148932$

边长为单位长的小双三角十二面截半二十面体，中分球半径为：

$R_{M}={\frac {6\left(5+{\sqrt {5}}\right)}{4}}\approx 1.647278207$

二面角

小双三角十二面截半二十面体共有两种二面角，分别为十边形面和三角形面的二面角、以及十边形面和五角星面的二面角。

其中，十边形面和三角形面的二面角角度约为100.8123度：

$\angle$十边形$,$三角形$\,=\arccos \left(-{\frac {\sqrt {15\left(5-2{\sqrt {5}}\right)}}{15}}\right)\approx 1.759506857578\approx 100.812316964^{\circ }$

而十边形面和五角星面的二面角为5平方根倒数的反馀弦值，角度约为63.43度：

$\angle$十边形$,$五角星$\,=\arccos \left({\frac {\sqrt {5}}{5}}\right)\approx 1.10714872\approx 63.4349488^{\circ }$

相关多面体

小双三角十二面截半二十面体与大星形截角十二面体共用相同的顶点布局。其亦与小十二面二十面体和小二十面化截半二十面体共用相同的边布局。

大星形截角十二面体

小二十面化截半二十面体

小双三角十二面截半二十面体

小十二面二十面体

拓朴

从组成元素来看，小双三角十二面截半二十面体似乎与大双三角十二面截半二十面体、小十二面截半二十面体和大十二面截半二十面体拓朴同构。但实际上与小双三角十二面截半二十面体拓朴同构的立体只有大双三角十二面截半二十面体。

参见

• 均匀多面体列表
• 完全扭棱二十面体