二十七面体

在几何学中，二十七面体是指有27个面的多面体，在实数空间中没有任何二十七面体是正多面体，但在其他空间中存在有由27个全等面组成的正多面体，例如在复数空间中，黑塞二十七面体是由27个全等的莫比乌斯－坎特八边形组成的正多面体。虽然实欧几里得空间中没有正二十七面体，但仍存在许多由正多边形组成的二十七面体，例如正五角罩帐柱、同相五角台塔丸塔和异相五角台塔丸塔。此外要构成二十七面体至少要有16个顶点。

二十七面体

部分的二十七面体
一种拟詹森二十七面体	正五角罩帐柱
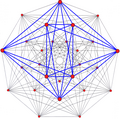黑塞二十七面体	同相五角台塔丸塔

正二十七面体

主条目：黑塞二十七面体

黑塞二十七面体，其中一个面以蓝色表示

实数空间中没有任何由27个面组成的正多面体，但在复数空间中有一种由27个全等的莫比乌斯－坎特八边形组成的正多面体，为黑塞二十七面体，其对偶多面体为本身。然而其位于复数空间中，因此并未出现于古典几何的五种正多面体当中。

常见的二十七面体

常见的二十七面体中有一些柱体与锥体以及部份的詹森多面体和卡塔兰立体。

二十六角锥

二十六角锥是一种底面为二十六边形的锥体，是二十七面体的一种，其具有27个面、52条边和27个顶点，其对偶多面体是自己本身。正二十六角锥是一种底面为正二十六边形的二十六角锥，在施莱夫利符号中可以用{}∨{26}来表示。底边长为$s$、高为$h$的正二十六角锥体积$V$和表面积$S$为：

$V={\frac {13hs^{2}\cot {\frac {\pi }{26}}}{6}}\approx 17.8441hs^{2}$

$S={\frac {13s\left({\sqrt {4h^{2}+s^{2}\cot ^{2}{\frac {\pi }{26}}}}+s\cot {\frac {\pi }{26}}\right)}{2}}\approx 6.5s\left({\sqrt {4h^{2}+67.8247s^{2}}}+8.23574s\right)$

二十五角柱

二十五角柱是一种底面为二十五边形的柱体，由27个面、75条边和50个顶点组成。正二十五角柱代表每个面都是正多边形的二十五角柱，其每个顶点都是2个正方形和1个二十五边形的公共顶点，顶点图以$4{.}4{.}25$表示。其在施莱夫利符号中可以用{25}×{}或t{2,25}来表示，在考克斯特符号中可以用来表示，在威佐夫符号中可以利用2 25 | 2来表示，在康威多面体表示法中可以利用P25来表示。底边长为$s$、高为$h$的正二十五角柱体积$V$和表面积$S$为：

$V={\frac {25hs^{2}\cot {\frac {\pi }{25}}}{4}}\approx 49.4738hs^{2}$

$S={\frac {25s\left(h+{\frac {s\cot {\frac {\pi }{25}}}{2}}\right)}{2}}\approx 25s\left(h+3.95791s\right)$

五角罩帐柱

主条目：正五角罩帐柱

五角罩帐柱是一种底面为五边形的罩帐柱，由27个面、55条边和30 个顶点组成。正五角罩帐柱是指每个面都是正多边形的五角罩帐柱，其是一种詹森多面体。

五角台塔丸塔

五角台塔丸塔是一种由五角台塔与五角丸塔组合成的多面体，由27个面、50条边和25个顶点组成。其根据组合方式的不同会有2种结果——同相五角台塔丸塔与异相五角台塔丸塔，这两种立体都是詹森多面体。

拟詹森多面体

部分拟詹森多面体具有27个面。

部分的拟詹森多面体因共面退化为二十七面体，例如二侧五角锥五角台塔丸塔。

二侧五角锥五角台塔丸塔

二侧五角锥五角台塔丸塔是指五角台塔丸塔的两个五边形面被五角锥取代所形成的立体，又可以分成二侧五角锥同相五角台塔丸塔和二侧五角锥异相五角台塔丸塔。当侧锥的五角锥为政五角锥时，这个立体将会出现8组三角形两两共面为菱形，进而退化为二十七面体。这样的立体共由8个菱形（共面退化）、9个三角形、5个正方形和5个五边形组成，共有27个面、52条边和27个顶点。

詹森多面体

部分詹森多面体具有27个面。

正五角罩帐柱 J21	同相五角台塔丸塔 J32	异相五角台塔丸塔 J33

二十七面体列表

名称	种类	图像	符号	顶点	边	面	χ	面的种类	对称性	展开图
黑塞二十七面体	复正多面体		3{3}3{3}3	27	72	27	-18	莫比乌斯－坎特八边形	L3 = 3[3]3[3]3, 648阶
二十五角柱	棱柱体		t{2,25} {25}x{}	50	75	27	2	2个二十五边形 25个矩形	D25h, [25,2], (*25 2 2), 100阶
二十六角锥	棱锥体		( )∨{26}	27	52	27	2	1个二十六边形 26个三角形	C26v, [26], (*26 26)
二十五角锥台	锥台			50	75	27	2	2个二十五边形 25个梯形	C25v, [25], (*25 25)
双九角锥柱	双角锥柱			20	46	27	2	18个三角形 9个四边形	D9h, [12,2], (*2 2 9), 36阶
	拟詹森多面体			18	43	27	2	23个三角形 3个四边形 1个五边形
	拟詹森多面体			17	42	27	2	24个三角形 3个四边形
正五角罩帐柱	詹森多面体			30	55	27	2	10个三角形 10个正方形 6个五边形 1个十边形	C5v
同相五角台塔丸塔	詹森多面体			25	50	27	2	15个三角形 5个正方形 7个五边形	C5v
异相五角台塔丸塔	詹森多面体			25	50	27	2	15个三角形 5个正方形 7个五边形	C5v
{6,3}(0,6)	正则地区图			54	81	27	0	六边形

参见

• 詹森多面体