九胞體
在幾何學中,九胞體是指有九個胞或維面的多胞體。若九個胞都全等且都為正圖形則為正九胞體。維度在七維和七維以下的所有多胞體中,沒有任何一個形狀是正圖形,換言之即八維以下不存在正九胞體,而八維空間中,八維單純形即是一種正九胞體。
| 部分的九胞體 | |
|---|---|
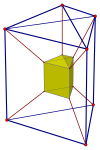 三角錐柱的四維柱體 (四維) |
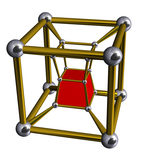 四角五角柱體柱 (四維) |
 三角錐柱體錐的五維錐體 (五維) |
 正九胞體 (八維) |
四維九胞體
编辑在四維空間中,九胞體為由9個多面體所組成的多胞體,例如八面體錐[1]、三角錐柱的四維柱體和四角五角柱體柱。
| 名稱 | 考克斯特 施萊夫利 |
胞 | 圖像 | 展開圖 |
|---|---|---|---|---|
| 八面體錐[2] | ( ) ∨ {3,4} | 1個正八面體 8個三角錐 |
||
| 四角五角柱體柱 | 4個五角柱 5個立方體 |
|||
| 三角錐柱 的四維柱體 |
2個三角錐柱 4個三角柱 3個四角柱 |
五維九胞體
编辑在五維空間中,九胞體為由9個四維多胞體所組成的多胞體,例如三角錐柱體錐的五維錐體。
| 名稱 | 考克斯特 施萊夫利 |
胞 | 圖像 | 展開圖 |
|---|---|---|---|---|
| 三角錐柱體柱錐 的五維錐體 |
2個三角錐柱的四維錐 3個四角錐的四維錐 4個五胞體 |
六維以上九胞體
编辑高維度的九胞體中,只有八維的單純形是一種正九胞體[3],除此之外並不存在其他正九胞體,但可以找到多種半正多胞體具有九個胞。
參見
编辑參考文獻
编辑- ^ Klitzing, Richard. 3D convex uniform polyhedra x3o4o - oct. bendwavy.org. 1/sqrt(2) = 0.707107
- ^ Klitzing, Richard. Segmentotope octpy, K-4.3. bendwavy.org.
- ^ Richeson, D.; Euler's Gem: The Polyhedron Formula and the Birth of Topoplogy, Princeton, 2008.