相對同時
在物理學中,同時性之相對性(英語:Relativity of simultaneity)是指超距同時性的概念並不是絕對的。換言之,在空間中不同位置所發生的事件,其同時性取決於觀測者所在的參考系。

簡述
编辑根據愛因斯坦的狹義相對論,發生在空間中不同位置的兩個事件,它們的同時性並不具有絕對的意義,我們沒辦法肯定地說它們是否為同時發生。若在某一參考系中此兩事件是同時的,則在另一相對於原參考系等速運動的新參考系中,此兩事件將不再同時(唯一的例外為新參考系的移動方向恰好垂直於兩事件空間位置的連線方向)。
舉例而言:現在有兩件事件分別為「一場發生在倫敦的車禍」與「一場發生在紐約的車禍」。對在地表上的某個觀測者來說,這兩個事件是同時發生的;但對另一個坐在飛機上的觀測者而言,這兩個事件發生的時間點將會有些微的不同。如果這兩個事件間沒有因果聯繫,則在某些參考系中會看見倫敦的車禍先發生,在另一些參考系中會看見紐約的車禍先發生。然而,若這兩事件間有因果聯繫,事件發生的先後順序則在每個參考系中都會相同。
歷史
编辑1895年,勞侖茲利用「本地時」(t' = t – v x/c2)的數學方法,解釋了邁克生-莫雷實驗的結果。但勞侖茲並沒有提出任何物理上的解釋[1],最終此解釋由龐加萊所給出。1898年,龐加萊在《時間的測量》這篇文章中也強調過本地時的效應,在此篇文章中龐加萊也說明了假定光速在各個方向上是常數的方便性。然而在這篇論文中並沒有針對勞侖茲理論的討論,亦未提及對於不同運動狀態的觀測者,同時性可能產生的問題[2][3]。
1900年,龐加萊運用光速在以太中不變的假設,成功導出「本地時」。由於「相對性原理」,在以太中等速運動的觀測者可以假設他們自身是靜止的,故光速在各個方向上就都會是定值(精確到v/c的一階項)。因此,若兩人想藉由光訊號使他們的時鐘同步,他們只需要考慮光訊號傳遞的時間,而不需要考慮觀測者本身相對以太的運動。所以移動中的時鐘是不同步的,它顯示的也不是「真正的時間」。龐加萊也計算了在時鐘同步時由於「本地時」效應所產生的誤差[4][5]。1904年,龐加萊在他的論文中強調了「相對性原理」、「本地時」、「光速的不變性」之間的關聯性,然而在這篇論文中龐加萊只有以定性與猜測的方式進行推演[6][7]。
1905年,愛因斯坦利用類似的方法導出了正確的時間轉換,也就是所謂的勞侖茲轉換。雖然龐加萊在1905年以前就得到了完整的時間轉換公式,但在龐加萊的論文中並沒有提及將時間同步的方法。愛因斯坦推導的基於光速不變性與相對性原理,所以愛因斯坦指出:對電動力學來說以太的存在是多餘的。因此,「真正的時間」和「本地時」的區別就消失了,所有時間都是同樣有效的,長度與時間的相對性就只是一個自然的結果[8][9][10]。
1908年,閔考斯基在他自己的閔考斯基空間模型中,引入了粒子世界線[11]的概念。閔考斯基空間的數學模型是一個仿射幾何的模型,此模型是以二次形來度量事件間的距離(當兩個事件由光所連繫時,它們的時空間距將為零)。在閔考斯基的系統裡,世界線上的每一個事件,都可以藉由二次形來決定出一個等時面,且這個等時面與粒子的運動速度有關。
思想實驗
编辑愛因斯坦的火車
编辑在愛因斯坦的思想實驗[12]中假設:有一位移動的觀測者坐在火車中央,有另一位靜止的觀測者站在月台上。在月台觀測者的參考系中,有三個事件同時但在不同地點發生。分別為:靜止觀測者恰好遇到移動觀測者(靜止觀測者與移動觀測者在火車移動方向上的位置座標相同時)、閃電打在火車頭上與閃電打在火車尾上。
由於這三個事件皆位於火車移動方向的軸上,因此它們的時間座標在移動參考系中將會變得不同。出現在火車前進方向上的事件將會比出現在反方向上的事件更早發生。因此在移動參考系中,閃電會先打到車頭上,之後兩個觀測者才會相遇。
火車與月台
编辑為了瞭解原因,我們可以考慮另一個著名的思想實驗。它與1910年丹尼爾·佛洛斯特·科姆斯托克[13]和1917年愛因斯坦所提出的思想實驗[12][14]類似。此實驗也有一個位於火車上的移動觀測者與另一個站在月台上的靜止觀測者。
當兩名觀測者相遇時,一道閃光從火車的中央發出。對火車上的觀測者而言,火車頭尾和光源的距離是固定的,所以光線會同時抵達火車的前端與後端。
另一方面,對站在月台上的觀測者而言,火車的尾端會朝向閃光的發射點靠近;火車的前端則會遠離閃光的發射點。所以只要光速是有限值且對所有觀測者來說是各向同性的,光走到火車後端的距離將會比走到前端的距離還短。因此,閃光就會在不同的時間點抵達火車的前後端。
時空圖
编辑利用時空圖來視覺化地呈現此情況,將會對此問題的理解有所幫助。對一給定的觀測者而言,t 軸是空間座標 x 的原點隨時間移動的軌跡,畫在時空圖上是鉛直的。x 軸則為t = 0時刻所有空間點所形成的集合,畫於時空圖上則為水平的。光速對所有觀測者都相同這一敘述意味著無論光源相對觀測者的速度為何,傾斜 45° 的直線一定是光信號的世界線。
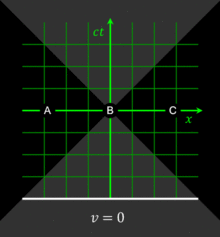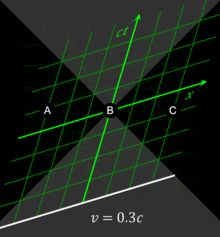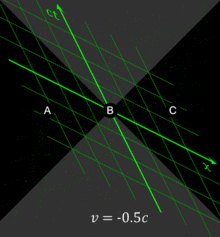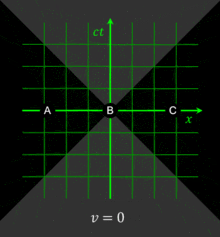
在第一張圖中,火車的頭尾以灰線表示。對火車上的觀測者而言,火車的頭尾是靜止的,因此這兩條線會是鉛直線。此點也顯示了火車頭尾的運動是在時間上的,而不是在空間上的。閃光則以傾斜 45° 的紅線表示。閃光打到火車頭尾的兩個時空點在時空圖上是等高的,此點顯示了這件兩事件是同時發生的。
在第二張圖中,火車的頭尾是朝右方移動的,在時空圖上則由兩條平行線所表示。閃光從火車的正中央發出,同樣也是由兩條傾斜 45° 的直線表示。在這張圖中,閃光打到火車頭尾的時空點不是等高的,所以這兩事件不是同時的。
勞侖茲轉換
编辑同時性之相對性的概念可藉由勞侖茲轉換來展現。勞侖茲轉換給出了在不同慣性參考系下事件座標的變換關係。
第一個參考系的座標由 t,x,y,z 表示,第二個參考系的座標由 t',x',y',z' 表示。假設兩參考系的座標軸都是平行的,以及他們的時空原點是相同的(t' = t = 0 時,兩空間座標的原點重合)。再假設相對第一個參考系,第二個參考系是沿著 x 方向以速度 v 運動。則以下的勞侖茲轉換展示了他們事件座標之間的聯繫
在此 c 為光速。如果有兩個事件在第一個觀測者的參考系中同時發生,他們會擁有相同的 t 座標。然而,若此兩事件擁有不同的 x 座標,他們就會有不同的 t' 座標,所以這兩事件在此參考系中不會同時發生。由於勞侖茲變換中有v x/c2 的項,因此造成了絕對同時性的破滅。
t' = 定值 的方程式定義了在第二個參考系中的「同時線」(在線上的所有事件都是同時發生的),就如同 t = 定值 的方程式定義了在第一個參考系中的「同時線」。從以上的勞侖茲轉換式中,我們可以發現 t' = 定值 等價於 t – v x/c2 = 定值。因此使 t 為定值的時空點所成的集合將與使 t' 為定值的集合不同。換言之,事件的同時性是取決於我們所關注的參考系。
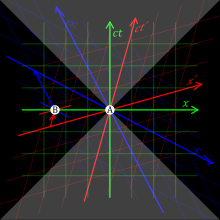
此點我們也可藉由時空圖的方法來表現出。我們可以考慮在時空圖上時間座標相同的時空點所形成的直線(同時線),此同時線是隨著觀測者而有所不同的。在右方的時空圖中,短劃線所表示的是以四分之一光速相對原點移動的觀測者所看見的同時線;水平的點虛線則表示相對原點靜止的觀測者所看見的同時線。此圖是以靜止觀測者的(x,t)座標所畫出的,並且在此光速等於1。換言之,一道光可由與 x 軸夾 45° 的直線表示。藉由前段的分析,給定 v = 0.25 及 c = 1,因此短劃線方程式為 t – 0.25x = 0;給定 v = 0,則點虛線方程式為 t = 0。
一般而言,第二個參考系的世界線(x' = 0)在第一個參考系中可由 t = x/v 描述;對第二個觀測者而言的同時線(t' = 0)在第一個參考系中則可由t = vx 描述。世界線與同時線之間的倒數關係事實上是與雙曲正交性有所關聯的。
加速觀測者
编辑以上關於勞侖茲轉換的計算使用了擴展同時性的定義(在事件發生的時間與地點,觀測者是不存在的),此概念在共動參考系或正切自由浮動參考系(tangent free-float-frame)的定義中也會被提及。我們只要使用雷達時(radar-time)定義的距離概念來給訂每一個事件的空間位置與時間座標,就可以將同時性的定義自然地推廣到發生在重力彎曲時空中或加速參考系底下的事件[15] 。
藉由擴展同時性的雷達時定義,可以幫助我們視覺化地呈現在沒有任何引力物體下的加速彎曲時空。在右圖中展示出了,當觀測者以固有加速度(紅色軌跡)運動時,在平坦時空中的事件雷達時等值線。關於此方法會產生的一個問題是,遠方事件的光尚未抵達觀測者之前,此事件的時間座標與空間位置都是沒有被定義的。
參見
编辑參考資料
编辑- ^ Lorentz, Hendrik Antoon, Versuch einer Theorie der electrischen und optischen Erscheinungen in bewegten Körpern, Leiden: E.J. Brill, 1895
- ^ Poincaré, Henri, The Measure of Time, The foundations of science, New York: Science Press: 222–234, 1898–1913
- ^ Galison, Peter, Einstein's Clocks, Poincaré's Maps: Empires of Time, New York: W.W. Norton, 2003, ISBN 0-393-32604-7
- ^ Poincaré, Henri, La théorie de Lorentz et le principe de réaction, Archives néerlandaises des sciences exactes et naturelles, 1900, 5: 252–278. See also the English translation (页面存档备份,存于互联网档案馆).
- ^ Darrigol, Olivier, The Genesis of the theory of relativity (PDF), Séminaire Poincaré, 2005, 1: 1–22 [2018-11-27], doi:10.1007/3-7643-7436-5_1, (原始内容存档 (PDF)于2018-11-08)
- ^ Poincaré, Henri, The Principles of Mathematical Physics, Congress of arts and science, universal exposition, St. Louis, 1904 1, Boston and New York: Houghton, Mifflin and Company: 604–622, 1904–1906
- ^ Holton, Gerald, Thematic Origins of Scientific Thought: Kepler to Einstein, Harvard University Press, 1988, ISBN 0-674-87747-0
- ^ Einstein, Albert, Zur Elektrodynamik bewegter Körper (PDF), Annalen der Physik, 1905, 322 (10): 891–921 [2018-11-27], Bibcode:1905AnP...322..891E, doi:10.1002/andp.19053221004, (原始内容存档 (PDF)于2015-09-24). See also: English translation (页面存档备份,存于互联网档案馆).
- ^ Miller, Arthur I., Albert Einstein’s special theory of relativity. Emergence (1905) and early interpretation (1905–1911), Reading: Addison–Wesley, 1981, ISBN 0-201-04679-2
- ^ Pais, Abraham, Subtle is the Lord: The Science and the Life of Albert Einstein, New York: Oxford University Press, 1982, ISBN 0-19-520438-7
- ^ Minkowski, Hermann, Raum und Zeit, Physikalische Zeitschrift, 1909, 10: 75–88
- Various English translations on Wikisource: Space and Time
- ^ 12.0 12.1 Einstein, Albert, Relativity - The Special and General Theory, READ BOOKS: 30–33, 2009, ISBN 1-4446-3762-2, Chapter IX (页面存档备份,存于互联网档案馆)
- ^ The thought experiment by Comstock described two platforms in relative motion. See: Comstock, D.F., The principle of relativity, Science, 1910, 31 (803): 767–772, Bibcode:1910Sci....31..767C, PMID 17758464, doi:10.1126/science.31.803.767.
- ^ Einstein's thought experiment used two light rays starting at both ends of the platform. See: Einstein A., Relativity: The Special and General Theory, Springer, 1917
- ^ Dolby, Carl E.; Gull, Stephen F. On radar time and the twin "paradox". American Journal of Physics. December 2001, 69 (12): 1257–1261. Bibcode:2001AmJPh..69.1257D. arXiv:gr-qc/0104077 . doi:10.1119/1.1407254.