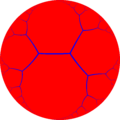
無限階三角形鑲嵌
在幾何學中，無限階三角形鑲嵌是一種位於雙曲平面仿緊空間鑲嵌圖形[1]，由正三角形組成，在施萊夫利符號中用{3,∞}來表示，考克斯特-迪肯符號中以
表示。每個頂點都是無限多個三角形的公共顶点[註 1]，也因此使這個圖形無法存於平面上。這個圖形每一條線都可以做為整個圖形的對稱線。
 龐加萊圓盤模型 | ||
| 類別 | 雙曲正鑲嵌 | |
|---|---|---|
| 對偶多面體 | 三階無限邊形鑲嵌 | |
| 識別 | ||
| 鮑爾斯縮寫 | aztrat | |
| 數學表示法 | ||
| 考克斯特符號 |    | |
| 施萊夫利符號 | {3,∞} | |
| 威佐夫符號 | ∞ | 3 2 | |
| 組成與佈局 | ||
| 頂點圖 | 3∞ | |
| 對稱性 | ||
| 對稱群 | [∞,3], (*∞32) | |
| 特性 | ||
| 點可遞、 邊可遞、 面可遞 | ||
| 圖像 | ||
| ||
無限階三角形鑲嵌可以視為一系列由三角形組成的多面體之幾何極限，但也可以達到更高階數，利用虛階數表示其階數比無窮大更多，即超無限階三角形鑲嵌，在考克斯特-迪肯符號中以
表示。
性質
编辑無限階三角形鑲嵌中，無限階指的是三角形的公共顶点的三角形個數為無限多個，由於每個頂點都是無限多個三角形的公共顶点[註 1]，因此最理想的狀態是每個頂點都位於龐加萊雙曲盤[註 2]投影的邊界上，即無窮遠處，否則將無法繪製出包含無限多個三角形的頂點。無限階三角形鑲嵌是三階無限邊形鑲嵌的對偶鑲嵌，因此每個三角形的公共顶点包含的三角形數量為可數集的數量，因此若要計算其角度總合的話將會計算出正無窮大[註 3]，有時會被記為 ，因為其為正三角形內角的整數倍，頂點圖以 或 表示每個頂點是無限多個三角形的公共顶点。
每個頂點都是無限多個三角形的公共顶点是一個抽象概念，其應視為正四面體（每個頂點都是三個三角形的公共顶点）、正八面體（每個頂點都是四個三角形的公共顶点）、正二十面體（每個頂點都是五個三角形的公共顶点）、正六邊形鑲嵌（每個頂點都是六個三角形的公共顶点）系列的極限，無限階三角形鑲嵌則為「頂點都是無限多個三角形的公共顶点」抽象概念被可視化的結果，因此無法於平面或一般常見的幾何學討論，只能在雙曲面幾何（羅氏幾何）中討論[2]。
由於無限階三角形鑲嵌是一個位於雙曲面上的形狀，因此要上它顯示於平面上必須使用投影，因此從不同位置投影出來的結果也不盡相同。下表列出一些不同位置投影的結果：
|
|
|
|
對稱群
编辑對稱性比較低的形式[註 4]就是在該圖形表面交替地塗上不同顏色，如下圖，以黃色及藍色交替上色，可以利用循環表式的考克斯特符號{(3,∞,3)}或威佐夫符號 來表示，也可以看成分別圖上三種顏色的鏡射線[註 5]，如下圖，以紅色、綠色以及藍色表示，他們代表了*∞∞∞對稱群的根本域。
 交錯塗色鑲嵌 |
 *∞∞∞對稱群 |
 Apollonian gasket與*∞∞∞對稱群 |
更高階數
编辑即使無限階已經是最多階數的了，但仍可以利用偽多邊形群構造更高階數的圖形，即階數使用虛數表示其所包含的三角形數量比無限大還要多。他們的對偶為三階超無限邊形鑲嵌，其邊數也是以iπ/λ[3]表示，代表其邊數比無限大還要多，同樣屬於非緊湊的雙曲鑲嵌，並且有無窮多種組合（整個虛數集）。
雖然是變為「超無限階」，但其實際上是變為每個頂點都不存在了，即不相交了，所組成的三角形則變成由三條在雙曲面上不將交的三條直線組成，如同無限面形中，二角形頂點因退化而不存在的情形，此三角形也是類似的情形。但由於三角形必須是由三條線段順次首尾相連，組成的一個閉合圖形，因此嚴格來說，那些三角形都不存在。
這些階數為複的三角形鑲嵌由於其形成了不閉合且不是有界的的空間，因此不屬於緊空間。
複階數的三角形鑲嵌也構成了一個無窮系列，從i、2i一直到虛無窮。也因此無限階三角形鑲嵌也可使視為兩個系列的極限。
| 類別 | 仿緊湊雙曲鑲嵌 | 非緊湊雙曲鑲嵌 | |||
|---|---|---|---|---|---|
| 階數 | 無限 | ∞i | ... | 12i | 11i |
| 圖像 |
|
|
... | 
|
|
| 頂點佈局 | 3∞ | 3∞i | ... | 312i | 311i |
| 類別 | 非緊湊雙曲鑲嵌 | ||||
| 階數 | 10i | 9i | 8i | 7i | 6i |
| 圖像 | 
|
|
|
|
|
| 頂點佈局 | 310i | 39i | 38i | 37i | 36i |
| 類別 | 非緊湊雙曲鑲嵌 | ||||
| 階數 | 5i | 4i | 3i | 2i | i |
| 圖像 | 
|
|
|
|
|
| 頂點佈局 | 35i | 34i | 33i | 32i | 3i |
相關多面體及鑲嵌
编辑在幾何學中，無限階三角形鑲嵌跟其他幾何圖形中有一些關聯，下面列出兩種關聯:同樣由三角形組成與無限變形鑲嵌的變換形。
三角形鑲嵌系列
编辑無限階三角形鑲嵌在拓撲上與一系列用施萊夫利符號{3,n}表示的（廣義）多面體一直延伸到雙曲鑲嵌擁有相似的結構：
| 多面体 | 欧式镶嵌 | 双曲镶嵌 | |||||||
|---|---|---|---|---|---|---|---|---|---|
 {3,2} |
 {3,3} |
 {3,4} |
 {3,5} |
 {3,6} |
 {3,7} |
 {3,8} |
 {3,9} |
... | {3,∞) |
這一系列圖形全部都是正圖形。在這一系列中，從n=2開始，n介於3到5是三維歐幾里得空間的多面體，這些面體同時也是柏拉圖立體，n為6時是歐幾里得平面鑲嵌圖，是正鑲嵌圖之一，n從7開始是二維羅氏幾何平面鑲嵌圖，即雙曲鑲嵌圖，直至無限大的無限階三角形鑲嵌，為此系列終點。
無限邊形鑲嵌的變換形
编辑無限階三角形鑲嵌可以透過三階無限變形鑲嵌透過對偶變換構成。其他可以經由無限邊形鑲嵌變換成的幾何圖形列於下表:
| 對稱群：[∞,3], (*∞32) | [∞,3]+ (∞32) |
[1+,∞,3] (*∞33) |
[∞,3+] (3*∞) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
 =  
|
=
|
=
|
|
=  or 
|
= or
|
= 
| ||||
|
|
|
|
|
|
|
|
|
||
| {∞,3} | t{∞,3} | r{∞,3} | t{3,∞} | {3,∞} | rr{∞,3} | tr{∞,3} | sr{∞,3} | h{∞,3} | h2{∞,3} | s{3,∞} |
| 半正對偶 | ||||||||||
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
||
| V∞3 | V3.∞.∞ | V(3.∞)2 | V6.6.∞ | V3∞ | V4.3.4.∞ | V4.6.∞ | V3.3.3.3.∞ | V(3.∞)3 | V3.3.3.3.3.∞ | |
| 對稱性: [(∞,3,3)], (*∞33) | [(∞,3,3)]+, (∞33) | ||||||
|---|---|---|---|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| {(∞,∞,3)} | t0,1{(∞,3,3)} | t1(∞,3,3) | t1,2(∞,3,3) | t2{(∞,3,3)} | t0,2(∞,3,3) | t0,1,2 {(∞,3,3)} | s(∞,3,3) |
| 對偶鑲嵌 | |||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
| V(3.∞)3 | V3.∞.3.∞ | V(3.∞)3 | V3.6.∞.6 | V(3.3)∞ | V3.6.∞.6 | V6.6.∞ | V3.3.3.3.3.∞ |
其他無限階三角形鑲嵌
编辑非正無限階三角形鑲嵌[註 6]可以從中央三角形經過境射的迭代過程中產生，如下圖所示：
參見
编辑
注釋
编辑參考文獻
编辑- ^ John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
- ^ Arlan Ramsay, Robert D. Richtmyer, Introduction to Hyperbolic Geometry, Springer; 1 edition (December 16, 1995)
- ^ Norman Johnson, Geometries and symmetries, (2015), Chapter 11. Finite symmetry groups, Section 11.2 The polygonal groups. p.141
- Chapter 10: Regular honeycombs in hyperbolic space. The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.