太陽路徑 编辑
太陽路徑是指由於地球環繞太陽的軌道造成太陽季節性的每小時位置變化 (和日照長度)。太陽的相對位置是影響建築物的太陽能系統獲得熱增益的性能最主要因素[1]。精確的知道太陽路徑和氣候條件是經濟的設置太陽能集熱器區域、定位、庭園設計、夏季遮陰、和太陽追蹤器等,不可或缺的專門知識[2][3]。

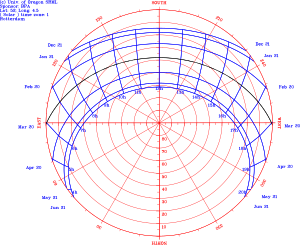
收集太陽能
编辑要有效的收集太陽能,太陽能收集器 (玻璃、太陽能電池板等) 必須在陽光直射角度範圍的20度以內。同時,也必須設置遮棚,這樣建築物在夏天才不會因為太熱而需要冷卻。與陽光的垂線偏離越遠,太陽增益越低,偏離垂線35度以上,會造成大部分的太陽光被太陽能集熱器的表面反射掉。
有效的太陽能系統 (被動太陽能、主動太陽能、建築物、設備等等),需要考慮到從夏天到冬天,太陽高度角和日出和日落在地平線上的太陽方位角 都會隨著季節產生47度,甚至更大的變化。
精確的知道太陽路徑需要準確的模型和數學預測,分析太陽能系統年均性能 - 來解釋,例如:為甚麼垂直於赤道面有最大的經濟效益?在冬季下雪與太陽高度很低時,關閉太陽能反射器的好處,和斜玻璃屋頂 (在溫室、天窗和暖房) 在夏天可以成為暖爐 (當太陽機乎垂直於玻璃時),而在冬天會失去比它所能收集到的更多的能量 (當太陽在地平線上的高度低於47度時,和在寒冷的冬天夜晚,溫暖的室內空氣會上升和從建築物內轉換熱到戶外)[1]。
地球的傾斜
编辑地球從一個極至另一個極的自轉軸相對於地球在太陽系繞太陽公轉的軌道平面傾斜約23.5度。當地球環繞著太陽時,這將在半球的冬天和夏天,創造出太陽高度角會有最大47度的具體區別。
在北半球,冬天的太陽從東南方升起,達到最大高度是低垂在南方地平線上,然後在西南方沒入。它整天都在建築物的南方 (赤道),垂直朝南的玻璃面是補獲太陽熱能的優良建材。
在南半球的冬天 (6月、7月和8月),太陽從東北方升起,幾乎會直接越過天頂 (具體取決於緯度),然後在西北方沒入。一個依據緯度設計面向赤道的簡單懸臂裝置可以很容易的在一年中最熱的日子將面向赤道的窗戶垂直進入的太陽增益百分百的直接阻絕掉。可捲動的外遮陽屏、室內半透明或不透明的窗簾、百葉窗、可移動的爬藤等 (沒有任何主動的電動空調),可以用來做為每天、每小時或季節性的熱傳輸控制。
緯度 (和半球) 特定的太陽路徑差異是被動式太陽能建築設計的關鍵。它們是設計適宜的窗戶和季節性旋臂最主要的資料。太陽能設計者必須精確的知道在他們的設計中,每個位置的太陽路徑角度,和如何比較依據季節的加熱和冷卻需求。
在美國,特定位置的太陽高度和方位角的季節性太陽路徑精確數值,可以從NOAA獲得 - 在北半球建築物的南側是朝向赤道,在南半球則是北方朝向赤道;同時太陽高度的峰值出現在夏至的6月21日 (最大值) 與冬至的12月21日 (最小值)。除了高緯度的冬季和夏季,在地球上的任何地點,太陽都大約是從東方升起,從西方沒入。
在赤道,每年的春分(大約3月21日)和秋分 (大約9月23日),太陽將在正午 (太陽時) 越過天頂並出現垂直的棍棒沒有影子的現象;在北緯23.5度的北回歸線,會在夏至日 (大約6月21日) 發生相同的現象。在一年中的其他日子,正午的影子將指向北極。同樣的,在赤道以南23.5度的南回歸線,會在南半球的夏至 (大約12月21日),出現垂直的棍棒在正午沒有影子的現象,並且在一年中其它的日子,正午的影子會指向南極。在北回歸線以北,正午的影子永遠指向北極;與此相反的,在南回歸線以南,正午的影子永遠指向南極。在北極圈和南極圈內,一年當中至少會有一天太陽會連續24小時不出現在地平線上,和連續在地平線上出現24小時 (六個月後)。
在適宜的緯度 (在極區和熱帶地區之間,大部份人類生活的地區),白天的長度、太陽的高度和方位、都隨著季節在變化。離赤道越遠,夏季漫長的白天相對於冬季簡短的白晝之間的差異也將越大[2]。
太陽路徑建築設計模擬
编辑在現代化之前,廉價的、3D電腦圖形、日影儀 (準確的可移動光源) 的物理模型被用來模擬建築物的太陽角度。今天,數學電腦模型計算特定位置的太陽增益 (遮屏) 和季節性的熱性能,並且有能力就提案的建築設計以旋轉和動畫呈現3D彩色圖模型。
被動式太陽能建築設計對加熱和冷卻問題是直覺的 (如屋頂傾斜的玻璃),精確的性能計算和模擬可以從本質上協助避免回顧和複製以前做過的昂貴實驗的建築錯誤 (像是夏天的太陽爐)。
參考資料
编辑- ^ Solar Resource Information. National Renewable Energy Laboratory. [2009-03-28]. (原始内容存档于2009-02-18).
- ^ 跳转到: 2.0 2.1 Khavrus, V.; Shelevytsky, I. Introduction to solar motion geometry on the basis of a simple model. Physics Education. 2010, 45 (6): 641 [2011-07-22]. doi:10.1088/0031-9120/45/6/010. (原始内容存档于2016-09-16).
- ^ Khavrus, V.; Shelevytsky, I. Geometry and the physics of seasons. Physics Education. 2012, 47 (6): 680 [2013-03-02]. doi:10.1088/0031-9120/47/6/680. (原始内容存档于2013-06-03).