因式分解
因式分解,在这里是指多項式因式分解(英語:Polynomial Factorization[註 1]),在數學中一般理解為把一個多項式分解為兩個或多個的因式[註 2]的過程。在這個過後會得出一堆較原式簡單的多項式的積。例如单元多項式可被因式分解為。又如二元多項式因式分解為。如果我们允许多項式系数从整数扩大到複整數,那么可被因式分解為。通常分解获得的每个因式要是不可约多项式(irreducible)。也就是不能再分解了。
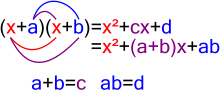
定义
编辑数域 上每个高于一次的多项式 都可以分解为该数域P上的多个不可约多项式 的乘积,为因式分解。
在复数域上,每个不可约多项式都是一次的,因此高于一次的复系数多项式,都可以唯一地分解为多个一次式之积。
在实数域上,不可约的多项式都是一次或二次的,因此高于一次的实系数多项式,都可以唯一地分解为一次、二次多项式之积。
在有理数域上,不可约多项式可以有任何次。例如,在有理数范围内,当 为正整数时,关于 的多项式 无法再分解[1]。
因式分解定理
编辑数域F上每个次数 的多项式 都可以分解成数域F上一些不可约多项式的乘积,并是唯一的,即如果有两个分解式
其中 和 都是数域F上的不可约多项式,那么必有 ,而且可以适当排列因式的次序,使得
,其中 是一些非零常数
分解方法
编辑公因式分解(抽)
编辑原则:
- 分解必須要彻底(即分解後之因式均不能再做分解)
- 結果最後只留下小括號
- 結果的多項式首項為正。
在一個公式內把其公因子抽出,例子:
-
- 其中, 是公因子。因此,因式分解後得到的答案是:
-
- 其中, 是公因子。因此,因式分解後得到的答案是:
公式法
编辑兩個立方數之和
兩個立方數之差
兩個n次方數之差
兩個奇數次方數之和
分组分解法
编辑透過公式重組,然後再抽出公因數,例子:
拆添项法
编辑透過添項然後減掉,然後再抽出公因數,例子:
或者透過分裂某項,然後再抽出公因數,例子:
其中, 可以被拆成 和 。所以, 可以被寫成 。因此,
其中, 可以被拆成 和 。所以, 可以被寫成 。因此,
十字交乘法
编辑十字交乘法(cross method),也叫做十字相乘法。它实際上是拆項法的一個變形,只不過用十字形矩陣來表示。
一次因式檢驗法
编辑一個整係數的一元多項式 ,假如它有整係數因式 ,且p,q互質,則以下兩條必成立:(逆敘述並不真)
不過反過來說,即使當 和 都成立時,整係數多項式 也不一定是整係數多項式 的因式
另外一個看法是:
一個整係數的n次多項式 ,若 是f(x)之因式,且p,q互質,則:(逆敘述並不真)
参见
编辑注释
编辑延伸閱讀
编辑- Burnside, William Snow; Panton, Arthur William (1960) [1912], The Theory of Equations with an introduction to the theory of binary algebraic forms (Volume one), Dover
- Dickson, Leonard Eugene (1922), First Course in the Theory of Equations, New York: John Wiley & Sons
- Fite, William Benjamin (1921), College Algebra (Revised), Boston: D. C. Heath & Co.
- Klein, Felix (1925), Elementary Mathematics from an Advanced Standpoint; Arithmetic, Algebra, Analysis, Dover
- Selby, Samuel M., CRC Standard Mathematical Tables (18th ed.), The Chemical Rubber Co








